
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Триадная система умножения. Триадная система умножения при вычислении использует структуры малой и трехмерной триад:
Триадная система умножения при вычислении использует структуры малой и трехмерной триад:

- малая триада (основание - 3)
-  трехмерная триада (основание - 4)
трехмерная триада (основание - 4)
Двухмерное триадное умножение.
Малая триада при данном умножении указывает на структуру, построение формы которой используется при вычислении.
При двухмерных триадных вычислениях, в качестве первого множителя, используется знак двухмерной триады - Zили z. Второй множитель указывает на количество рядов в триаде. Результатом же является количество точек в получившейся триаде.
 |




 Z * 2 \ Z2 = 3
Z * 2 \ Z2 = 3
| |||
 | |||






 Z * 3 \ Z3 = 6
Z * 3 \ Z3 = 6
 |

|
|
Z * 6 \ Z6 = 21
 Z * 7 \ Z7 = 28
Z * 7 \ Z7 = 28
Z * 8 \ Z8 = 32
Z * 9 \ Z9 = 41
Z * 10 \ Z10 = 51
Z * 11 \ Z11 = 66
Z * 12 \ Z12 = 78
Z * 13 \ Z13 = 91
Z * 14 \ Z14 = 105
Z * 15 \ Z15 = 120
Z * 16 \ Z16 = 136
Трехмерное триадное умножение.
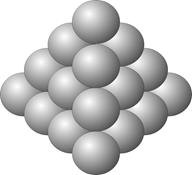
При трехмерных триадных вычислениях, в качестве первого множителя, используется знак объемной триады - eили знак z, если задано трехмерное умножение знаком ЖДЫ (&). Второй множитель указывает на количество рядов в триаде. Результатом является количество точек в получившейся триаде.
 |


 z & 2 \ e2 = 4
z & 2 \ e2 = 4
 |


|

 z & 3 \ e2 = 10
z & 3 \ e2 = 10
 | |||
 |
|
| z & 5 \ e5 = 35 | z & 11 \ e11 = 286 |
| z & 6 \ e6 = 56 | z & 12 \ e12 = 364 |
| z & 7 \ e7 = 84 | z & 13 \ e13 = 455 |
| z & 8 \ e8 = 120 | z & 14 \ e14 = 560 |
| z & 9 \ e9 = 165 | z & 15 \ e15 = 680 |
| z & 10 \ e10 = 220 | z & 16 \ e16 = 816 |
 В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
en ≡ en-1 + Zn
Дело в том, что трехмерная триада состоит из соединенных между собой плоскостями малыми триадами, у которых длины сторон увеличиваются на единицу по порядку возрастания номеров рядов в трехмерной триаде (если рядом номер один считать самый верхний ряд). Например структура трехмерной триады сформированная умножением триадно жды три (e3 ) состоит из следующих малых триад:
 |

Ряд №1 = 1
|
Ряд №2 - Z2 = 3
Ряд №3 - Z3 = 6
 |
Триадно жды четыре получается путем «добавления снизу» еще одной малой триады, длина стороны которой будет уже равна четырем, т.е.:

 | |||
 | |||
 |  | ||||||
 | |||||||
 | |||||||
Если при вычислении таблиц трехмерного триадного умножения не брать в расчет таблицы двухмерного умножения, то путем нехитрых вычислений можно получить еще одну формулу:
 |
en ≡ en-1 - en-2 + en-1 + n
Например:
e5 ≡ e5-1 - e5-2 + e5-1 + 5 = e4 - e3 + e4 + 5 = 20 – 10 + 20 + 5 = 35
Не нашли, что искали? Воспользуйтесь поиском: