
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Призменная система умножения
Данная система умножения, так же как и Пирамидальная изначально является трехмерной. Существуют две системы Призменного умножения, построенные на применении следующих структур:
1) Малая Призма, обозначаемая знаком - u


|
2) Ровная Призма, обозначаемая знаком - r
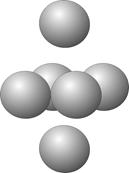

|
Умножение Малой Призмы
При вычислении Малой Призмы следует учесть, что:
полной разверткой указывается количество рядов в Призме и данное число всегда нечетное,
 например - u & 3
например - u & 3
 |
сокращенной разверткой указывается количество визуальных основ,
 например - u2
например - u2
 |
|

 u2 \ u & 3 = 5
u2 \ u & 3 = 5
 |
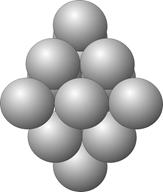
|
При умножении Малой Призмы результат есть сумма Малой Триады в основании и двух Трехмерных Триад.


Соответственно, результат можно вычислить
по следующей формуле:
 |
un \ u & (n * 2 - 1) = zn + en-1 + en-1
или (зная результат предыдущей Малой призма жды)
 |
un \ u & (n * 2 - 1) = un-1 + zn-1 + zn
| u4 \ u & 7 = 30 | u11 \ u & 21 = 506 |
| u5 \ u & 9 = 55 | u12 \ u & 23 = 650 |
| u6 \ u & 11 = 91 | u13 \ u & 25 = 819 |
| u7 \ u & 13 = 140 | u14 \ u & 27 = 1015 |
| u8 \ u & 15 = 204 | u15 \ u & 29 = 1240 |
| u9 \ u & 17 = 285 | u16 \ u & 31 = 1496 |
| u10 \ u & 19 = 385 |
Умножение Ровной Призмы
При вычислении Ровной Призмы, так же как и при Малой:
полной разверткой указывается количество рядов в Призме и данное число всегда нечетное,
 например - r & 3
например - r & 3
 |
сокращенной разверткой указывается количество визуальных основ,
 например - r2
например - r2
 |

|
 r2 \ r & 3 = 6
r2 \ r & 3 = 6
 |

|
При Ровно Призменном умножении малая (двухмерная) Ровна суммируется с двумя Пирамидами, имеющими множители на единицу меньше.


Формулы вычисления «Ровно призма жды»:
 |
rn = r & (n * 2 – 1) = yn + xn-1 + xn-1
или (опять же зная результат предыдущей
Ровно призма жды):
 |
rn = r & (n * 2 – 1) = rn-1 + yn + yn
| r4 \ r & 7 = 44 | r11 \ r & 21 = 891 |
| r5 \ r & 9 = 85 | r12 \ r & 23 = 1156 |
| r6 \ r & 11 = 146 | r13 \ r & 25 = 1469 |
| r7 \ r & 13 = 231 | r14 \ r & 27 = 1834 |
| r8 \ r & 15 = 344 | r15 \ r & 29 = 2255 |
| r9 \ r & 17 = 489 | r16 \ r & 31 = 2736 |
| r10 \ r & 19 = 670 |
Не нашли, что искали? Воспользуйтесь поиском: