В) Решить данную систему методом обратной матрицы.

Решение. Данную систему можно записать в матричном виде АХ = В,

где , ,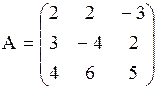

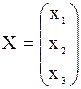Решение матричного уравнения имеет вид Х = А^-1 В = N, где А^-1 – матрица, обратная матрицы А. Так как определитель матрицы системы D(A) = 180 отличен от нуля то матрица А имеет обратную. Для вычисления обратной матрицы воспользуемся формулой

Где А₁₁, А₁₂, …, А₃₃ – алгебраические дополнения элементов а₁₁, а₁₂, …, а₃₃ матрицы А. Вычислим алгебраические дополнения всех элементов матрицы А:

; ; ;

; ;

; ; .

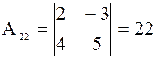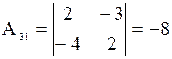Составим обратную матрицу

.

Найдем теперь матрицу Х.

Из равенства матриц Х = N или 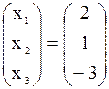следует решение системы

х₁=2, х₂ = 1, х₃ = -3.

Задача 2. Методом исключения неизвестных найти общее и базисное

решение системы линейных уравнений

Решение.

Это система двух уравнений с тремя неизвестными. Она совместна и неопределенна. Надо описать совокупность всех ее решений. В качестве базисных неизвестных данной системы можно взять те неизвестные, для которых определитель составленный из коэффициентов при нет известных, не равен нулю. Здесь три таких определителя, один из которых равен нулю . Следовательно, неизвестные х₁ и х₂ нельзя брать в качестве базисных. Примем за базисные неизвестные х₁ и х₂, для которых определитель . Будем считать неизвестную х₃ свободной и запишем систему в виде

Или в матричной форме . Воспользуемся методом полного исключения неизвестных:

Общее решение: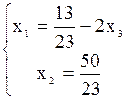

Полагая в общем решении х₃ = 0, получим базисное решение х₁ = ,

Проверка базисного решения показывает, что оно удовлетворяет обоим уравнениям системы, то есть, является частным решением системы. Давая х₃ любые другие числовые значения, получим бесчисленное множество частных решений.

Аналогично решаются системы с несколькими свободными неизвестными.

Задача 3. Даны матрицы и . Найти

произведение матриц АВ.

Решение.

Эти матрицы являются соответственными, так как число столбцов первой матрицы равно числу строк второй: их размеры и . В результате умножения матриц получим новую матрицу С размера 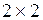, а ее элементы будут равны скалярным произведениям векторов-строк первой матрицы на векторы-столбцов второй:

Задача 4. Даны вершины треугольника А(-3;-2), В(1;8), С(5;3).

Найти: а) уравнения всех трех его сторон;

б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;

в) внутренний угол А треугольника в градусах и минусах;

г) длину высоты, опущенной из вершины А;

д) площадь треугольника.

Решение.

а) Уравнения сторон найдем по формуле прямой, проходящей через две данные точки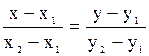

Уравнение стороны АВ: 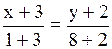, или (АВ).

Уравнение стороны АС: или (АС)

б) Каждая из прямых, уравнения которых только это найдены, разделяет плоскость на две полуплоскости, определяемые соответствующими неравенствами.

Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств. определяющих множество внутренних точек треугольника.

Рис. 1.

Система неравенств определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.

в) Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле .

Угловые коэффициенты прямых выложим по формуле .

Получим ; .

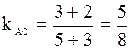Тогда

. Угол определяем с помощью таблицы тангенсов или калькулятора

г) Длину высоты AD^BC (рис. 1) найдем как расстояние от данной точки А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле

, где А, В, С – коэффициенты прямой, - координаты данной точки.

Получим (мин. ед.)

д) Площадь треугольника можно вычислить несколькими способами.

Вычислить ее через координаты вершин треугольника по формуле .

Получим .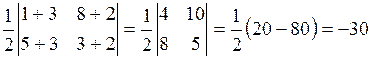

Итак, площадь треугольника S_ABC = 30 кв. ед.

Задачи раздела ΙΙ заданий (см. оглавление, п.5.2)

Задача 5. Найти производные 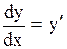следующих функций (дается

сложные и неявная функции):

а)

Решение.

Не нашли, что искали? Воспользуйтесь поиском: