
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Найдем частные производные

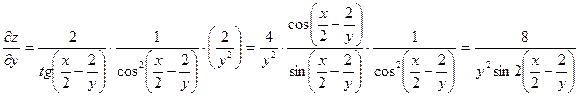 .
.
Составим полный дифференциал
 .
.
Задача 10. Найти экстремум функции 
Решение.
Найдем частные производные: 
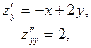
и смешанную производную  .
.
Необходимое условие экстремума:  и
и 
Решим систему уравнений  x = 2y, 4y – y = -9, y = -3
x = 2y, 4y – y = -9, y = -3
x = -9
Итак, точка P(-9; -3) критическая точка. Составим выражение 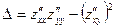 и вычислим его значение в критической точке P(-9; -3). Тогда, если
и вычислим его значение в критической точке P(-9; -3). Тогда, если 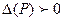 , то P- точка экстремума. При этом, если
, то P- точка экстремума. При этом, если  , то Р – точка минимума,
, то Р – точка минимума,
а если  , то Р – точка максимума,
, то Р – точка максимума,
Если 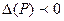 , экстремума нет, а если
, экстремума нет, а если  - экстремум может быть, а может не быть. Нужны дополнительные исследования.
- экстремум может быть, а может не быть. Нужны дополнительные исследования.
Установим характер экстремума в точке P(-9; -3).
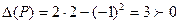 , следовательно, P(-9; -3)- точка экстремума, а так как
, следовательно, P(-9; -3)- точка экстремума, а так как  независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции.
независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции.
Задача 11. Найти неопределенные интегралы а)  , б)
, б)  ,
,
в) 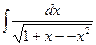 , г)
, г)  , д)
, д)  .
.
Предлагаемые интегралы можно, применив основные методы
интегрирования; метод замены переменной подстановка, метод
интегрирования по частям.
Решение.
а)  ;
;
Подстановка:  . Найдем дифференциалы обеих частей подстановки
. Найдем дифференциалы обеих частей подстановки 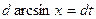
или  . Произведем замену переменной в подынтегральном выражении и найдем интеграл
. Произведем замену переменной в подынтегральном выражении и найдем интеграл  .
.
б) 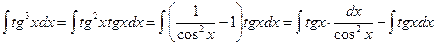 .
.
В первом из интегралов, стоящих справа, введем подстановку 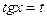 . откуда
. откуда 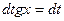 или
или  . Таким образом,
. Таким образом,  .
.
Второй интеграл справа является табличным  .
.
Итак, 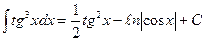 , где
, где  , две произвольные постоянные суммы неопределенных интегралов объединяют в одну.
, две произвольные постоянные суммы неопределенных интегралов объединяют в одну.
в) 
Подстановка: 
Получим табличный интеграл типа 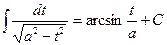 . Возвращаясь к прежней переменной, будем иметь
. Возвращаясь к прежней переменной, будем иметь  .
.
г)  . Найдем его методом интегрирования по частям по формуле
. Найдем его методом интегрирования по частям по формуле 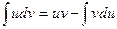 .
.
Примем  ,
, 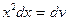 .
.
В первом из этих двух равенств обе части дифференцируем, чтобы найти 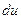 , а во втором интегрируем, чтобы найти
, а во втором интегрируем, чтобы найти  . Получим
. Получим  ,
,  (здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения
(здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения  ).
).
Применив формулу интегрирования по частям, получим
 .
.
д)  . Это интеграл от рациональной функции. Разложим подынтегральную функцию
. Это интеграл от рациональной функции. Разложим подынтегральную функцию 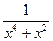 на простейшие дроби по известному правилу, предварительно разложив знаменатель дроби на множители
на простейшие дроби по известному правилу, предварительно разложив знаменатель дроби на множители 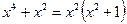 . Тогда
. Тогда 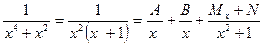 , где A, B, M, N – неопределенные коэффициенты, которые надо найти. Приведя обе части последнего равенства к общему знаменателю, найдем
, где A, B, M, N – неопределенные коэффициенты, которые надо найти. Приведя обе части последнего равенства к общему знаменателю, найдем
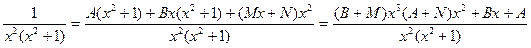 .
.
Такое равенство отношений с одинаковыми знаменателями возможны только в случае равенства числителей, то есть  .
.
Приравнивая коэффициенты при x в одинаковых степенях в левой и правой частях последнего равенства, получим систему уравнений
 Решение системы:
Решение системы: 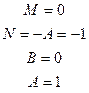
Переходим к интегрированию
!!  .
.
Приведем две задачи геометрического характера, связанные с вычислениями определенного интеграла.
Задача 12. Вычислить площадь фигуры, ограниченной линиями  ,
,
 ,
,  (рис.2)
(рис.2)
Решение.
Фигура ОМА (рис.4) ограниченная данными линиями, состоит из двух частей ОМВ и ВМА, представляющих собою частные случаи криволинейных трапеций, ограниченных сверху кривой  на на  и примой и примой  на на  . Таким образом искомая площадь вычисляется с помощью определенного интеграла как сумма двух площадей по формуле . Таким образом искомая площадь вычисляется с помощью определенного интеграла как сумма двух площадей по формуле 
|
рис. 4.
Определенные интегралы вычисляются по ф>рмуле Ньютона-Лейбница  . Итак, площадь ОМА равна
. Итак, площадь ОМА равна
 .
.
Задача 13. Вычислить объем тела, полученного в результате вращения
вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  ,
,  ,
,
 ,
,  . (рис. 5).
. (рис. 5).
Решение.
Объем тела вращения находим по формуле

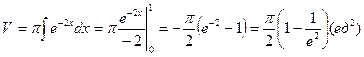
|
рис. 5.
Задача 14. Найти частное решение дифференциального уравнения
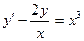 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
 при
при 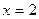 .
.
Решение.
Это уравнение первого порядка является линейным, так как это удовлетворяет общему виду линейных уравнений  . Будем искать решение в виде
. Будем искать решение в виде  , где
, где 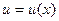 ,
,  - дифференцируемые функции от
- дифференцируемые функции от  . Тогда
. Тогда  . Подставляя
. Подставляя  ,
,  в данное уравнение, получим
в данное уравнение, получим

или  .
. 
Приравняем нулю выражение, стоящее в скобках и получим уравнение с разделяющимися переменными  или
или  , или
, или  . Интегрируя обе части уравнения, находим
. Интегрируя обе части уравнения, находим  или
или  (Здесь полагают произвольную постоянную равной нулю). Откуда
(Здесь полагают произвольную постоянную равной нулю). Откуда 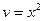 . Подставляя его уравнение
. Подставляя его уравнение  , придем к его общему уравнению с разделяющимися переменными
, придем к его общему уравнению с разделяющимися переменными  или
или  , или
, или  , или
, или  , откуда
, откуда  .
.
А так как решение ищется в виде  , то оно будет таким
, то оно будет таким 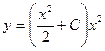 . Это- общее решение, в котором
. Это- общее решение, в котором  - произвольная постоянная. Решим теперь задачу Коши: из общего решения по заданным начальным условиям определим частное решение. Для этого подставим в общее решение начальные условия. Получим
- произвольная постоянная. Решим теперь задачу Коши: из общего решения по заданным начальным условиям определим частное решение. Для этого подставим в общее решение начальные условия. Получим  или
или  , или
, или  , или
, или  , откуда
, откуда  . Подставляя это значение постоянной в общее решение, получим частное решение
. Подставляя это значение постоянной в общее решение, получим частное решение  удовлетворяющее начальным условиям.
удовлетворяющее начальным условиям.
Задача 15. Найти область сходимости степенного ряда  .
.
Решение.
Область сходимости называется множество всех точек сходимости данного ряда. Найдем радиус и интервал сходимости.
 .
.
Где  . Радиус сходимости
. Радиус сходимости 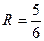 . Тогда интервал сходимости
. Тогда интервал сходимости  . Исследуем сходимость ряда на концах этого интервала.
. Исследуем сходимость ряда на концах этого интервала.
1) Подставим в данный степенной ряд  . Получим числовой ряд
. Получим числовой ряд 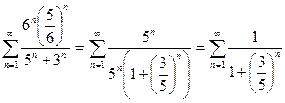 . Этот ряд является расходящимся, так как не выполняется необходимое условие его сходимости
. Этот ряд является расходящимся, так как не выполняется необходимое условие его сходимости 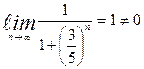 .
.
2) Подставляя в степенной ряд  , получим знакочередующийся числовой ряд
, получим знакочередующийся числовой ряд 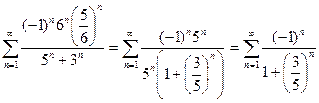 , который расходится по той же причине: его общий член при
, который расходится по той же причине: его общий член при 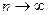 стремится к 1, а не к 0.
стремится к 1, а не к 0.
Итак, область сходимости данного степенного ряда  .
.
Не нашли, что искали? Воспользуйтесь поиском: