Обычный симплекс- метод

Симплексом в пространстве n переменных называют выпуклый много- гранник, имеющий n +1 вершину. В пространстве двух переменных это тре- угольник, в пространстве трех переменных - тетраэдр. В обычном симплекс- методе используется правильный симплекс (все ребра которого равны).

Идея симплекс-метода, которая далее рассматривается на примере дву- мерного случая, заключается в следующем. Выбирается начальный симплекс с вершинами x (1)- x (2)- x (3). Размещение правильного симплекса в пространстве может быть осуществлено двумя путями (рис.1).

x 2

x (3)

x ц.т.

x (4)

x (2)

Q

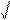
x (1)

P x 1

Рис. 1

В общем случае координаты вершин симплекса определяются матрицей:

n +1 + n −1);

n 2

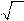
Q = 1 (

n +1 −1).

n 2

x 2 x (3)

x (1)

R 1 V 1

Рис. 2

x 1

x (2)

В общем случае координаты вершин симплекса определяются матрицей:

n Ri

= 1;

2 ⋅ i (i +1)

Vi =

i.

2(i +1)

В первом и во втором случаях формулы получены для симплекса, длина ребра которого равна единице. Для произвольной длины каждую формулу нужно умножить на длину ребра. Если поиск осуществляется не из начала координат, а из начальной точки x (0), то к координатам вершин симплекса необходимо добавить координаты начальной точки- x 1(0) и x 2(0).

В вершинах исходного симплекса рассчитывается значение целевой функции f (x (1)), f (x (2)), f (x (3)). Из этих трех значений выбирается "наихудшая" точка (при поиске минимума это та точка, в которой функция принимает мак- симальное значение). Допустим, что это точка x (1). Через центр тяжести проти- волежащей грани x ц.т.=(x (2) + x (3))/2 строится новая вершина симплекса x (4), сим- метричная "наихудшей" вершине x (1) (рис.1). Координаты новой вершины x (4) рассчитываются по формуле:

x (4)= x ц.т.+ (x ц.т.- x (1))= x (2) + x (3) - x (1)

В результате получается новый симплекс x (2) - x (3) - x (4), причем значение целевой функции в двух точках x (2) и x (3) уже известно. Поэтому вычисляется

значение функции в точке x (4) и среди всех вершин ищется вершина с "наихуд- шим" значением. Эта вершина вновь отображается через середину противоле- жащей грани и вся процедура повторяется. Признаком окончания поиска явля-

ется так называемая процедура зацикливания, когда вновь отображенная вер- шина оказывается "наихудшей". В этом случае, если заданная точность не дос- тигается, (точность определяется длиной ребра симплекса) необходимо умень- шить размеры симплекса. Процедура повторяется до тех пор, пока длина ребра

симплекса не станет меньше заданной точности.

В общем n – мерном случае, если обозначить отображаемую вершину симплекса за x (1), остальные вершины - x (2), x (3), x (n +1), отображенную вершину за x (n +2), координаты центра тяжести грани, относительно которой производится отображение, определяются по формуле:

n +1

x ц.т.

= 1 ∑ x (i), а отображаемой вершины

n i =2

x (n +2) = x

ц.т.

+α(x

ц.т.

− x (1)). (4.1)

Здесь множитель α > 0. При α =1 получаем зеркальное отображение x (1) и если

исходный симплекс был правильным, то при зеркальном отображении и новый

симплекс окажется правильным.

Не нашли, что искали? Воспользуйтесь поиском: