Преобразование матрицы линейного оператора к диагональному виду.

Наиболее простой вид принимает матрица A линейного оператора Ã, имеющего n линейно независимых собственных векторов e ₁, e ₂, …, e_n с собственными значениями, соответственно равными λ₁, λ₂, …, λ _n. Векторы e ₁, e ₂, …, e_n примем за базисные. Тогда Ã (e_i) = λ _ie_i (i = 1, 2, …, n) или

à (e_i) = a _{1 i} e ₁ + a _{2 i} e ₂ + … + a_iie_i + … + a_nie_n = λ _ie_i,

откуда a_ij = 0, если i ¹ j, и a_ii = λ _i, если i = j. Таким образом, матрица оператора Ã в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:

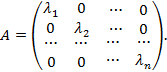
Верно и обратное: если матрица A линейного оператора Ã в некотором базисе является диагональной, то все векторы этого базиса – собственные векторы оператора Ã.

Если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.

Не нашли, что искали? Воспользуйтесь поиском: