
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Комплексная плоскость. Тригонометрическая форма комплексного числа.
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:

Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.
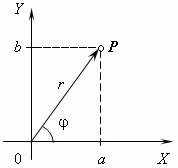
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
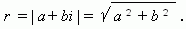
Сопряжённые комплексные числа имеют одинаковый модуль. __
Аргумент комплексного числа - это угол 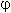 между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan 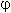 = b / a.
= b / a.
Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент 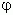 :
:
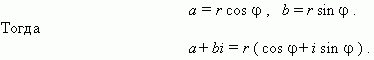
Не нашли, что искали? Воспользуйтесь поиском: