Интегральная кривая. Начальные условия. Дифференциальные уравнения с разделяющимися переменными.

Дифференциальное уравнение первого порядка y' = f (x,y) называется уравнением с разделяющимися переменными, если функцию f (x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p (x) и h (y) − непрерывные функции.
Рассматривая производную y' как отношение дифференциалов , перенесем dx в правую часть и разделим уравнение на h (y):

Разумеется, нужно убедиться, что h (y) ≠ 0. Если найдется число x ₀, при котором h (x ₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h (y) приводит к потере указанного решения.
Обозначив , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.

Вычисляя интегралы, получаем выражение

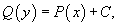
описывающее общее решение уравнения с разделяющимися переменными.

Не нашли, что искали? Воспользуйтесь поиском: