Формула Лиувилля-Остроградского

Пусть функции y ₁, y ₂,..., y_n образуют фундаментальную систему решений дифференциального уравнения n -го порядка. Предположим, что точка x ₀ принадлежит отрезку [ a, b ]. Тогда для определителя Вронского справедлива формула Лиувилля-Остроградского:

где a ₁ − коэффициент перед производной y ^{(n - 1)} в дифференциальном уравнении. Здесь мы считаем, что коэффициент a ₀(x) перед y ⁽ⁿ⁾ в дифференциальном уравнении равен 1. В противном случае формула Лиувилля-Остроградского принимает вид:

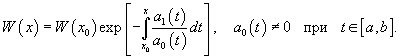
Не нашли, что искали? Воспользуйтесь поиском: