
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Умножение вектора на число
Додавання
Якщо дано дві матриці m -на- n A і B, можемо означити їх суму A + B як матрицю m -на- n, що утворюється додаванням відповідних елементів, себто,
(A + B)[ i, j ] = A [ i, j ] + B [ i, j ]. Наприклад,
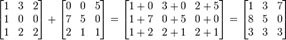
Множення на скаляр
Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[ i, j ] = cA [ i, j ]. Наприклад,
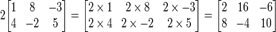
З цими двома операціями множина M(m, n, R) усіх матриць m -на- n з дійсними елементами є дійсним векторним простором розмірності mn.
Множення матриць
Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m -на- n (m рядків, n стовпчиків), а B — матриця n -на- p (n рядків, p стовпчиків), їх добуток AB є матрицею m -на- p (m рядків, p стовпчиків), що розраховується за формулою:
(AB)[ i, j ] = A [ i, 1] * B [1, j ] + A [ i, 2] * B [2, j ] +... + A [ i, n ] * B [ n, j ] для кожної пари i та j.
Наприклад,
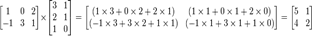
Це множення має такі властивості:
· (AB) C = A (BC) для всіх матриць A розмірності k -на- m, B розмірності m -на- n і C розмірності n -на- p (асоціативність).
· (A + B) C = AC + BC для всіх матриць A і B розмірності m -на- n і матриць C розмірності n -на- k (дистрибутивність).
· C (A + B) = CA + CB для всіх матриць A і B розмірності m -на- n і матриць C розмірності k -на- m (дистрибутивність).
2.Визначник або детермінант — вираз складений за певним законом з n² елементів квадратної матриці. Одна з найважливіших характеристикквадратних матриць.
Для квадратної матриці розміру 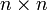 визначник є многочленом степеня
визначник є многочленом степеня  від елементів матриці, і є сумою добутків елементів матриці зі всіма можливими комбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановки номерів.
від елементів матриці, і є сумою добутків елементів матриці зі всіма можливими комбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановки номерів.
Якщо елементами матриці є числа, то визначник — також число. Взагалі, визначник може бути функціональним або належати якомуськомутативному кільцю, залежно від походження матриці.
З точністю до знака, визначник матриці виражає коефіціент, на який множаться  -мірні об'єми під дією цієї матриці.
-мірні об'єми під дією цієї матриці.
Визначник 2×2 матриці
Щоб знайти визначник  матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі:
матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі:

Визначник 3×3 матриці
Щоб знайти визначник  матриці, будуємо шість добутків таким чином:
матриці, будуємо шість добутків таким чином:
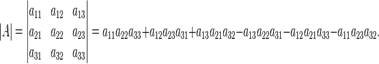 Для знаходження визначників високого порядку застосовуються принципово інші методи (насамперед, метод Гауса), що вимагають значно меншої кількості арифметичних операцій
Для знаходження визначників високого порядку застосовуються принципово інші методи (насамперед, метод Гауса), що вимагають значно меншої кількості арифметичних операцій 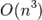 замість
замість  ).
).
Властивості
1,Якщо помножити якийсь рядок на константу 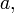 то визначник також помножиться на
то визначник також помножиться на 
2,Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.
3,При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.
4,У матриці з двома однаковими/пропорційними рядками або з нульовим рядком, визначник дорівнює нулю.
5,Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.
6,Визначник трикутної матриці дорівнює добутку елементів на діагоналі.
7,Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.
8,Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.
9, 
10, 
11, 
3.Мінором  -го порядку матриці
-го порядку матриці  називається визначник матриці, утворений елементами на перетині
називається визначник матриці, утворений елементами на перетині  стовпців та
стовпців та  рядків.
рядків.
Нехай 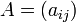 — матриця розміру
— матриця розміру 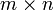 , в якій вибрано довільні
, в якій вибрано довільні 
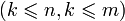
· рядків з номерами  та
та
· стовпців з номерами 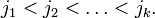
Елементи, що знаходяться на перетині обраних рядків та стовпців утворюють квадратну матрицю порядку  .
.
Алгебраїчне доповнення мінора 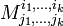 визначається так:
визначається так:

де

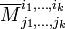 — доповнювальний мінор.
— доповнювальний мінор.
Алгебраїним доповненням елемента 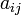 називають мінор цього елемента, взятий зі знаком
називають мінор цього елемента, взятий зі знаком
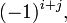 тобто
тобто

Одинична матриця — квадратна матриця розміру  з одиницями на головній діагоналі та нулями у всіх інших елементах.
з одиницями на головній діагоналі та нулями у всіх інших елементах.
Зазвичай позначається як  , іноді з індексом, що вказує розмірність:
, іноді з індексом, що вказує розмірність:  .
.
Одинична матриця належить до
· діагональних,
· ортогональних,
· додатноозначених,
· ортогонально-проекційних матриць
· та бінарних матриць.
Обернена матриця — матриця (позначається 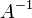 ), яка існує для кожної невиродженої квадратної матриці
), яка існує для кожної невиродженої квадратної матриці  , розмірності
, розмірності 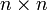 , причому:
, причому:
· 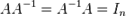
· де  одинична
одинична  матриця.
матриця.
· Якщо для матриці  існує
існує  , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.
, то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.
Точні методи
· Метод Гауса — Жордана
· LU розклад матриці
·  де
де 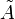 — союзна матриця.
— союзна матриця.
Приклади:
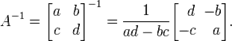
Обернена матриця існує тоді і тільки тоді, коли  .
.
4.Матричний метод роз’язання лінійних систем.
Нехай дано систему: 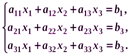
Розглянемо три матриці: 
Перша матриця називається матрицею симтеми, друга матрицею-стовпцем змінних, третя – матрицею-стовпцем вільних членів. Тоді систему можна записати у матричному вигляді:  . Якщо матриця системи рівнянь невироджена
. Якщо матриця системи рівнянь невироджена 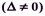 , то розв’язок системи знаходимо у вигляді
, то розв’язок системи знаходимо у вигляді 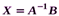 , або
, або 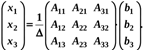
5.Метод Крамера. Цей метод розв’язування систем лінійних рівнянь зводиться до обчислення визначників. Так, розв’язок системи (2.1) можна знайти за формулами Крамера:

де 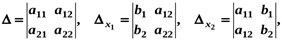 за умови, що
за умови, що 
 - називається визначником системи (2.1), а
- називається визначником системи (2.1), а  - визначники, які дістають з визначника
- визначники, які дістають з визначника  заміною першого, другого стовпців відповідно стовпцем вільних членів.
заміною першого, другого стовпців відповідно стовпцем вільних членів.
Формули Крамера для системи (2.2) мають вигляд: 
де 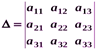
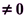 - визначник системи (2.2), а
- визначник системи (2.2), а
 визначники, які дістають з визначника
визначники, які дістають з визначника  заміною першого, другого і третього стовпців відповідно стовпцем вільних членів.
заміною першого, другого і третього стовпців відповідно стовпцем вільних членів.
Системи (2.1) і (2.2) мають:
а) єдиний розв’язок, коли 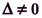 ;
;
б) безліч розв’язків, коли 
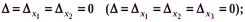
в) не мати жодного розв’язку, коли 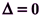 і хоча б один із визначників
і хоча б один із визначників 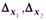
 відмінний від нуля.
відмінний від нуля.
6.Декартову систему координат (або прямокутна система координат) вперше запропонував відомий французький математик Рене Декарт близько 1637 р. у праці «Геометрія», одному з додатків до видатного філософського твору «Міркування про метод».
Сучасна Декартова система координат в двох вимірах (також знана під назвою прямокутна система координат) задається двома осями, розташованими під прямим кутом одна до одної. Площину, в якій знаходяться осі, називають іноді xy -площиною. Горизонтальна вісь позначається як x (вісь абсцис), вертикальна як y (вісь ординат). В тривимірному просторі до цих двох додається третя вісь, перпендикулярна xy -площині — вісь z. Всі точки в системі Декартових координат, складають так званий Декартовий простір.
Точка перетину, де осі зустрічаються, називається початком координат та позначається як O. Відповідно, вісь x може бути позначена як Ox, а вісь y — як Oy. Прямі, проведені паралельно до кожної осі на відстані одиничного відрізку (одиниці виміру довжини) починаючи з початку координат, формують координатну сітку.
Точка в двовимірній системі координат задається двома числами, які визначають відстань від осі Oy (абсциса або х-координата) та від осі Ох (ордината або y-координата) відповідно. Таким чином, координати формують впорядковану пару (кортеж) чисел (x, y). В тривимірному просторі додається ще z-координата (відстань точки від ху-площини), та формується впорядкована трійка координат (x, y, z).
Вибір букв x, y, z походить від загального правила найменування невідомих величин другою половиною латинського алфавіту. Букви першої його половини використовуються для іменування відомих величин.
Стрілки на осях відображають те, що вони простягаються до нескінечності в цьому напрямі.
Перетин двох осей створює чотири квадранти на координатній площині, які позначаються римськими цифрами I, II, III, та IV. Зазвичай порядок нумерації квадрантів — проти годинникової стрілки, починаючи з правого верхнього (тобто там, де абсциси та ординаті — позитивні числа). Значення, яких набувають абсциси та ординати в кожному квадранті, можна звести в наступну таблицю:
7.Рівняння прямої на площині
Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду
A x + B y+ C = 0
Де A і B не можуть одночасно дорівнювати нулю.
Рівняння прямої в відрізках на осях
| x | + | y | = 1 |
| a | b |
Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках
8.Рівняння прямої на площині
Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду
A x + B y+ C = 0
Де A і B не можуть одночасно дорівнювати нулю.
Рівняння прямої, що проходить через дві різні точки на площині
Якщо пряма проходить через дві точки A(x1, y1) і B(x2, y2), такі що x1 ≠ x2 і y1 ≠ y2 то рівняння прямої можна знайти, використовуючи наступну формулу
| x- x1 | = | y-y1 |
| X2 - x1 | y2 - y1 |
9.Рівняння прямої на площині
Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду
A x + B y+ C = 0
Де A і B не можуть одночасно дорівнювати нулю.
Рівняння прямої в відрізках на осях
| x | + | y | = 1 |
| a | b |
Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках
10. Пряма лінія — алгебраїчна лінія першого порядку: у декартовій системі координат пряма лінія задається на площині рівнянням першого степеня (лінійне рівняння):

де 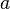 ,
, 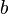 ,
,  — деякі числа, при чому
— деякі числа, при чому 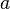 або
або 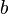 повинне бути відмінне від нуля.[1] Це рівняння - загальне рівняння прямої. Його також називають «стандартним».
повинне бути відмінне від нуля.[1] Це рівняння - загальне рівняння прямої. Його також називають «стандартним».
Натомість, Канонічне рівняння прямої, що випливає з попереднього має вигляд лінійної функції:
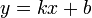 .
.
Пряма (а також пара пересічних прямих) є виродженим прикладом конічного перетину.
11. Якщо дві прямі перетинаються, вони утворюють чотири кути. Кутова міра не найбільшого з них називається кутом між двома прямими, що перетинаються. Величина кута між прямими, що перетинаються, не перевищує 90°.Кут між прямими a та b позначають символом ∠ ab.
Кут між прямими в просторі не фігура, а кутова міра, величина. Якщо прямі паралельні або збігаються, то кут між ними дорівнює 0°.
Паралельні прямі ніколи не перетинаються.
Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним прямим. Величина кута між мимобіжними прямими не перевищує 90°.
Дві прямі називаються перпендикулярними, якщо кут між
ними дорівнює 90°.
12. Якщо дано загальне рівняння прямої, то щоб привести його до нормального виду треба усі його складові помножити на нормуючий множник ϻ(мю)
Знак нормального множника обирається протилежним знаку вільного члена рівняння


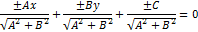

Нормальне рівняння прямої
13. Для визначення відстані від точки до прямої необхідно знати рівняння прямої і координати точки в декартовій системі координат. Відстанню від точки до прямої буде перпендикуляр, проведений із цієї точки до прямої.
Вам знадобиться
координати точки і рівняння прямої
1. Загальне рівняння прямої в декартових координатах має вигляд Ax + By + C = 0, де A, B і C - відомі числа. Нехай точка O має координати (x1, y1) в декартовій системі координат.
В цьому випадку відхилення цієї точки від прямої одно? = (Ax1 + By1 + C)/sqrt (A ^ 2) + (B ^ 2), якщо C<0, і? = (Ax1 + By1 + C)/(-sqrt (A ^ 2) + (B ^ 2), якщо C>0.
Відстань від точки до прямої - це модуль відхилення точки від прямої, тобто r = | (Ax1 + By1 + C)/sqrt (A ^ 2) + (B ^ 2) |, якщо C<0, і? = | (Ax1 + By1 + C)/(-sqrt (A ^ 2) + (B ^ 2) |, якщо C>0.
2. Нехай тепер точка з координатами (x1, y1, z1) задана в тривимірному просторі. Пряма може бути задана параметрично, системою з трьох рівнянь: x = x0 + ta, y = y0 + tb, z = z0 + tc, де t - дійсне число. Відстань від точки до прямої можна знайти як мінімальне від цієї точки до довільної точки прямої. Коефіцієнт t цієї точки дорівнює tmin = (a (x1-x0) + b (y1-y0) + c (z1-z0)/(a ^ 2) + (b ^ 2) + (c ^ 2)
3. Відстань від точки (x1, y1) до прямої можна порахувати і в разі, якщо пряма задана рівнянням з кутовим коефіцієнтом: y = kx + b. Тоді рівняння перпендикулярній їй прямий буде мати вигляд: y = (-1/k) x + a. Далі потрібно врахувати, що ця пряма повинна проходити через точку (x1, y1). Звідси знаходиться число a. Після перетворень знаходиться і відстань між точкою і прямою.
14. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором. (Перемещение, сила, скорость и т.д.)
Обозначения: 
Геометрический вектор – это направленный отрезок.
Для вектора 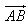
точка А – начало, точка В – конец вектора.
Модуль вектора – это длина отрезка AB. Вектор, модуль которого равен нулю, называется нулевым.
Два вектора называются равными, если они сонаправленные и имеют равные модули.
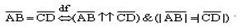
Равные векторы можно обозначать одной буквой (с чертой или со стрелкой): 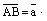
Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора 
не будет равна 7 м.
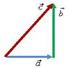
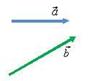 Для того, чтобы построить вектор
Для того, чтобы построить вектор 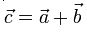 применяются специальные правила сложения векторов.
применяются специальные правила сложения векторов.
А длину вектора суммы 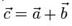 определяют по теореме косинусов
определяют по теореме косинусов 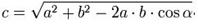 где α, – угол между векторами
где α, – угол между векторами 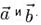
Если слагаемые векторы путем их параллельного переноса последовательно пристраивать один за другим так, что начало последующего вектора, совпадает с концом предыдущего, то вектор, замыкающий получившуюся ломаную, является суммой данных слагаемых, причём его начало совпадает с началом первого из слагаемых векторов, а конец – с концом последнего. На рисунке показано сложение четырёх векторов a, b, c и d. Символически это записывается в виде равенства f = a + b + c + d, где вектор f и является суммой указанных векторов.
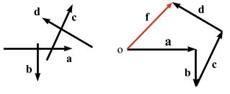
При сложении двух векторов часто используют так называемое «правило параллелограмма». При этом строят параллелограмм, используя слагаемые векторы в качестве его смежных сторон. Диагональ параллелограмма, проведённая из точки, где соединяются начала векторов, и является искомой суммой
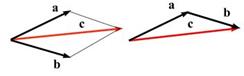
Легко видеть, что это правило приводит к тому же результату, что и указанный выше способ. При сложении более двух векторов «правило параллелограмма» практически не используется из-за громоздкости построений. Сложение векторов коммутативно, то есть, а + b = b + а.
И еще, сумма определенного числа векторов не зависит от порядка, в котором они складываются, то есть, (а + b) + d = a + (b + d). В этом случае говорят, что сложение векторов ассоциативно, то есть для него выполняется сочетательный закон.
Умножение вектора на число
Произведение вектора 
на число λ называется вектор 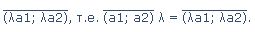
Для любого вектора a и чисел λ, μ

Для любого вектора a и b и числа λ
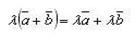
Не нашли, что искали? Воспользуйтесь поиском: