
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Перша важлива границя
Перша важлива границя
Розглянемо функцію 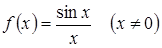 . Значення цієї функції при
. Значення цієї функції при  не існує, але
не існує, але 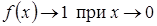 .
.
Теорема 2.1. Справедлива рівність
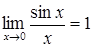 .
.
28.неперервність функції.теореми про властивості функцій неперервних у точці.класифікація точок розриву функцій
Функція  називається неперервною в точці
називається неперервною в точці  :
:
1) якщо функція  , визначена в точці
, визначена в точці  ;
;
2) якщо існує гра
ниця 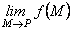 в точці
в точці  ;
;
3) якщо границя функції дорівнює значенню функції в цій точці, тобто. 
Разом всі ці умови є необхідними і достатніми для того, щоб функція  була неперервною в точці.
була неперервною в точці. 

30. похідною функції - у=f (x) в точці х0 називається границя відношення приросту (дельта у) функції до приросту (дельта х) аргументу за умови, що границя існує. А приріст (дельта х)аргументу прямує до 0.
Механічний зміст похідної полягає в її застосуванні при знаходженні швидкості  , кутової швидкості
, кутової швидкості  , питомої теплоємності
, питомої теплоємності  за відомими законами зміни відстані
за відомими законами зміни відстані  , кута
, кута  , кількості теплоти
, кількості теплоти  методом диференціювання останньої величини. Таким чином, взявши похідну від певної фізичної змінної ми можемо знайти швидкість її зміни. Похідна від закону зміни швидкості при прямолінійному русі буде рівна прискоренню тіла, а також і другою похідною від закону зміни відстані
методом диференціювання останньої величини. Таким чином, взявши похідну від певної фізичної змінної ми можемо знайти швидкість її зміни. Похідна від закону зміни швидкості при прямолінійному русі буде рівна прискоренню тіла, а також і другою похідною від закону зміни відстані  , тобто
, тобто


Гео.зміст
Значення похідної функції  в точці
в точці  рівне кутовому коефіцієнту (тангенсу кута нахилу) дотичної, проведеної до графіка функції в точці з абсцисою
рівне кутовому коефіцієнту (тангенсу кута нахилу) дотичної, проведеної до графіка функції в точці з абсцисою 

В цьому означенні і полягає геометричний зміст похідної.
Константа
 , де
, де 
Сума і різниця похідних


Похідна від добутку і частки


Похідна від складної функції

Похідна від оберненої функції

Похідні від простих функцій

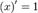

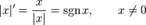
 , де
, де 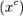 та
та  - визначені
- визначені
Зокрема:

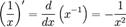

Похідні від експоненціальних і логарифмічних функцій
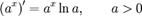



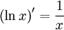
Похідні від тригонометричних функцій
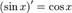



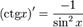




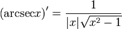
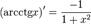

Похідні від гіперболічних функцій


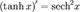
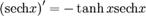








32.Логарифмічне диференціювання
Означення 1. Логарифмічною похідною функції називається похідна від логарифма цієї функції  .
.
Для знаходження похідної степенево-показникової функції  має сенс застосовувати логарифмічне диференціювання.
має сенс застосовувати логарифмічне диференціювання.
Нехай 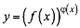 . Якщо спочатку прологарифмувати за основою
. Якщо спочатку прологарифмувати за основою  обидві частини рівності:
обидві частини рівності:  , а потім продиференціювати, враховуючи, що
, а потім продиференціювати, враховуючи, що 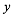 є функцією
є функцією  , то отримаємо
, то отримаємо
 .
.
Звідки  або, якщо згадати вигляд
або, якщо згадати вигляд 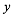 , то
, то
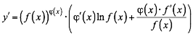 .
.
33. 
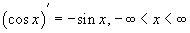


34. Під похідною вищих порядків розуміють диференціювання функції більше ніж один раз. Якщо похідну  повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції
повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції  , і вона позначається
, і вона позначається

Похідна третього порядку матиме вигляд

Аналагічно отримують формули для знаходження похідних вищих порядків. При знаходженні похідної  порядку необхідно знати похідну
порядку необхідно знати похідну  -го порядку. Вийняток становлять функції, для яких можна помітити тенденцію зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:
-го порядку. Вийняток становлять функції, для яких можна помітити тенденцію зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:

В інших випадках, для знаходження похідних вищих порядків від заданої функції потрібно послідовно знаходити всі її похідні нижчих порядків.
Таблица основных интегралов

Інтеграл — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі. Існує кілька різновидів визначених інтегралів: інтеграл Рімана, інтеграл Лебега, інтеграл Стілтьєса тощо.
37. Диференціал невизначеного інтеграла дорівнюе підінтегрально-му виразу, тобто d I /[x)dx = f\x)dx.
Дійсно, за означенням невизначеного інтеграла маємо ^f(x)dx = F(x) + C, де F'{x) = f(x)
38.Основні властивості визначеного інтервала
Властивість 1. Постійний множник можна виносити за знак визначеного інтегралу: якщо  , то
, то
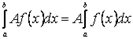 .
.
Властивість 2. Визначений інтеграл від алгебраїчної суми декількох функцій рівний алгебраїчній сумі інтегралів від доданків
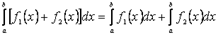 .
.
Властивість 3. Якщо на відрізку  де
де  , функції
, функції  і
і  задовольняють умові
задовольняють умові 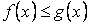 , то
, то
 .
.
Властивість 4. Якщо  і
і  - найменше і найбільше значення функції
- найменше і найбільше значення функції  на відрізку
на відрізку  і
і 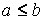 , то
, то
 .
.
Властивість 5 (теорема про середнє). Якщо функція  неперервна на відрізку
неперервна на відрізку  , то на цьому відрізку знайдеться така точка
, то на цьому відрізку знайдеться така точка 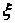 , що справедлива рівність
, що справедлива рівність
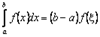 .
.
Властивість 6. Для будь-яких чисел  справедлива рівність
справедлива рівність
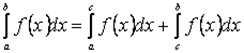 ,
,
39.інтегрування частинами у визначеному інтервалі

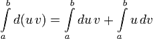

40. Диференційні рівняння. Загальний розв'язок



Диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів. Задача Коші — одна з основних задач теорії диференціальних рівнянь полягає в пошуку розв'язку (інтеграла) диференціального рівняння, що задовольняє початковим умовам (початковим даним).
Задача Коші зазвичай виникає при аналізі процесів, обумовлених диференціальним законом і початковим станом, математичним виразом яких і є рівняння та початкова умова (звідси й термінологія та вибір позначень: початкові дані задаються при 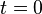 , а розв'язок знаходиться при
, а розв'язок знаходиться при  ).
).
Звичайне диференціальне рівняння першого порядку, розвязане відносно похідної:

41. Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду

де 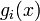 та
та 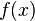 — функції, що залежать тільки від аргументу x.
— функції, що залежать тільки від аргументу x.
Важливий підклас лінійних диференційних рівнянь складають лінійні диференційні рівняння зі сталими коефіцієнтами, для яких 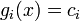 .
.
Рівняння

називається однорідним лінійним диференційним рівнянням.
Однорідне диференційне рівняння n-го порядку має n лінійно незалежних розв'язків.
Якщо відомий хоча б один частковий розв'язок лінійного диференційного рівняння, то його загальний розв'язок є сумою часткового розв'язку та лінійної комбінації n розв'язків однорідного диференційного рівняння.

покладемо  , що дає
, що дає

Діленням на  многочлен n-го порядку
многочлен n-го порядку

Це алгебраїчне рівняння 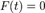 , характеристичне рівняння, було розглянуто пізніше Ґаспаром Монжем і Оґюстеном-Луї Коші.
, характеристичне рівняння, було розглянуто пізніше Ґаспаром Монжем і Оґюстеном-Луї Коші.
Формально, члени

42. Теорія ймовірностей — розділ математики, що вивчає закономірності випадкових явищ: випадкові події, випадкові величини, їхні функції, властивості і операції над ними. Математичні моделі в теорії ймовірностей описують з деяким ступенем точності випробування (експерименти, спостереження, вимірювання), результати яких неоднозначно визначаються умовами випробування. Подія — зміна властивостей об'єкта, взаємодія між об'єктами, утворення нового об'єкта або знищення існуючого об'єкта. Кожна подія містить оцінку часу, що вказує, коли воно відбувається, і місця, де вона відбувається. Події поділяються на: правдиві (однозначно відбудуться), неможливі, випадкові, сумісні, несумісні. Позначаються великими латинськими літерами, наприклад, А, B, С.
43. Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай, скінченної множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку.
Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття. Перестановкою скінченної множини 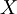 називається довільна бієктивна функція
називається довільна бієктивна функція 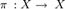 . Всього існує
. Всього існує  (факторіал) різних перестановок, де
(факторіал) різних перестановок, де 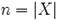 (потужність множини (кількість елементів в ній)). В комбінаториці, розміщенням із n елементів по m, або впорядкованою (n, m) вибіркою із множини M (потужність n, m ≤ n) називають довільний кортеж
(потужність множини (кількість елементів в ній)). В комбінаториці, розміщенням із n елементів по m, або впорядкованою (n, m) вибіркою із множини M (потужність n, m ≤ n) називають довільний кортеж  що складається із m попарно відмінних елементів.
що складається із m попарно відмінних елементів.
44. Ймові́рність (лат. probabilitas, англ. probability) — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Імовірність є основним поняттям розділу математики, що називається теорія імовірностей. Геометрична ймовірність — це поняття ймовірності, що запроваджується так: Нехай  — деяка підмножина прямої, площини чи простору. Випадкова подія
— деяка підмножина прямої, площини чи простору. Випадкова подія  — підмножина
— підмножина  . Тоді ймовірність випадкової події визначається формулою:
. Тоді ймовірність випадкової події визначається формулою: 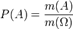 де
де 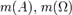 — довжина, площа чи об'єм множин
— довжина, площа чи об'єм множин  та
та  .
.
Це пов'язане з інтерпретацією ймовірності як міри на обраному просторі елементарних подій. В даному випадку він збігається з евклідовим простором.
46. У теорії ймовірностей дві випадкові події називаються незалежними, якщо настання однієї з них не змінює вірогідність настання іншої. Аналогічно, дві випадкові величини називають незалежними якщо значення однієї з них не впливає на розподіл значень іншої. Для незалежних подій формула спрощується і приймає вже відомий вигляд: Р(АВ) = Р(А)·Р(В)
47.формула повної ймовірності. Формула Баєса
р (AHi) = р (Hi) р (A | Hi) = р (A) р (Hi | A) –формула повної ймовірності.  - формула Баеса
- формула Баеса

49.Закон розподілу пуассона. Ймовірність відхилення….
 закон розподілу пуассона.
закон розподілу пуассона.
p (∣ ∣ nm − p ∣ ∣ <ε)=2Φ(ε√ npq) – відхилення
50. Локальна теорема Лапласа Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции.
51. Інтегральна теорема Лапласа Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна р(р≠1;р≠0). Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, 
52.Числові характеристики дискретних випадкових величинМатематическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности М (Х) = х 1 р 1 + х 2 р 2 + … + хпрп. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:  Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания D (X) = M (X – M (X))².
Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания D (X) = M (X – M (X))².
53.


54. Статистична сукупність – безліч одиниць, що володіють масовістю, типовістю, якісної однорідністю і наявністю варіації.
варіація — відносна міра дисперсії випадкової величини
Варіанта - це окреме значення ознаки, яке вона приймає в ряду розподілу.
55. Генеральна та вибіркова сукупності. Варіаційні та… Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов. Генеральной (основной) совокупностью называют совокупность, объектов из которых производится выборка.
В результате статистической обработки материалов можно подсчитать число единиц, обладающих конкретным значением того или иного признака. Каждое отдельное значение признака будем обозначать x1,x2 и называть вариантой, а абсолютное число, показывающее, сколько раз встречается та или иная варианта, — частотой и обозначать m1,m2,.Если отдельные значения признака (варианты) расположим в возрастающем или убывающем порядке и относительно каждой варианты укажем, как часто она встречается в данной совокупности, то получим статистическое распределение признака, или вариационный ряд. Он характеризует изменение (варьирование) какого-нибудь количественного признака. Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, в другой — частоты.
56. Середня арифметична - це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:
Хсер = (x1 + x2 + … + xn) / n = ∑x / n.
Середня квадратична використовується для визначення показників варіації (коливання) ознаки - дисперсії та середнього квадратичного відхилення. Обчислюється на основі квадратів відхилень індивідуальних значень ознаки від їх середньої величини. Формула середньої квадратичної має такий вигляд:
- проста: Хсер = √x2 / n
- зважена: Хсер = √x2f / ∑f
Середня гармонічна — це обернена до середньої арифметичної із обернених значень ознак. її обчислюють, коли необхідно осереднення обернених індивідуальних значень ознак шляхом їх підсумування (наприклад, у випадках визначення середніх витрат часу, праці, матеріалів на одиницю продукції тощо). У випадку розрахунку середньої гармонічної зваженої її обчислюють тоді, коли відомі дані про загальний обсяг ознаки (z = xf), а також індивідуальні значення ознаки (х), невідома є частота (f). Формули середньої гармонічної - простої і зваженої — мають такий вигляд:
- для простої: Хсер = n / ∑1 / x
- для зваженої: Хсер =∑z / ∑z / x
Середню геометричну застосовують у тих випадках, коли обсяг сукупності формується не сумою, а добутком індивідуальних значень ознак. Цей вид середньої використовується здебільшого для обчислення середніх коефіцієнтів (темпів) зростання в рядах динаміки. Так, у випадку однакових часових інтервалів між рівнями динамічного ряду середня геометрична проста має такий вигляд:
kсер = n√k1 * k2 *…*kn
де k = yi / yi-1 - темпи зростання; уi, уi-1 - відповідно розглядаємий та попередній рівні ряду; n— кількість інтервалів.
Середня кубічна величина застосовується при визначенні середнього
розміру об’ємних ознак – xQ. Вона дорівнює кореню кубічному із суми кубів
варіант, віднесеної до їх загальної кількості.
57. Правило мажорантності середніх: чим вище показник ступеня m, тим більше величина середньої.

57. варіація це відмінність у значеннях якої небудь ознаки в різних одиниць даної сукупності у той самий період або момент часу. Показники варіації характеризують коливання окремих значень. Існує декілька видів показників: 1.середнє лінійне відхилення, 2.дисперсія(показник варіації,що виражає середнє квадратичне відхилення, від середніх величин залежно від утвореного варіаційного фактору).3. середнє кВ.відхилення
58. Кореляційною залежністю між двома змінними називається функціональна залежність між значеннями однієї з них та умовним математичним сподіванням іншої.
Кореляційна залежність може бути представлена у вигляді
Mx(Y)=φ(x)
MY(X)=ψ(y) (1)
де φ(x)≠const, ψ(y)≠const.
Кореляційний аналіз — це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation — взаємозв'язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному — їх багатовимірні комплекси (групи).[1]
Мета кореляційного аналізу — виявити чи існує істотна залежність однієї змінної від інших.
Головні завдання кореляційного аналізу:
1. оцінка за вибірковими даними коефіцієнтів кореляції
2. перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення
3. оцінка близькості виявленого зв'язку до лінійного
4. побудова довірчого інтервалу для коефіцієнтів кореляції.
59. лінійна кореляція та лінійна регресія
лінійна регресія — це метод моделювання залежності між скаляром y та векторною (у загальному випадку) змінною X. У випадку, якщо змінна X також є скаляром, регресію називають простою.Для усунення недоліку коваріації був введений лінійний коефіцієнт кореляції (або коефіцієнт кореляції Пірсона), який розробили Карл Пірсон, Френсіс Еджуорт і Рафаель Уелдон (Англ.) рос. в 90-х роках XIX століття. Коефіцієнт кореляції розраховується за формулою [10] [8]:

Коефіцієнт кореляції змінюється в межах від мінус одиниці до плюс одиниці [11].
Доказ
Розділивши обидві частини подвійного нерівності  на
на  одержимо
одержимо

Лінійний коефіцієнт кореляції пов'язаний з коефіцієнтом регресії у вигляді такої залежності:  де
де 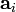 - Коефіцієнт регресії,
- Коефіцієнт регресії,  - Середньоквадратичне відхилення відповідного факторного ознаки
- Середньоквадратичне відхилення відповідного факторного ознаки
60. коефіцієнт кореляції ті його властивості
Коефіцієнт кореляції
Нехай  та
та  — випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як
— випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як  і дорівнює:
і дорівнює:

де:
 — коваріація величин
— коваріація величин  та
та  ,
,
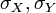 — стандартне відхилення величин
— стандартне відхилення величин  та
та  ,
,
 — оператор математичного сподівання.
— оператор математичного сподівання.
Властивості
Якщо X та Y — незалежні, то коефіцієнт кореляції 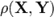 дорівнює 0. Зворотне твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X.
дорівнює 0. Зворотне твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X.
Завжди виконується нерівність:
 .
.
Причому,  тоді і лише тоді, коли
тоді і лише тоді, коли  , де a та b — сталі.
, де a та b — сталі.
61.Коефіціент прямолінійної регресії. Рівняння лінійної регресії
Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.
Якщо для кожного набору значень X 1 = x 1, X 2 = x 2,..., X p = x p визначено умовне математичне сподівання
y (x 1, x 2,..., x p) = E (Y | X 1 = x 1, X 2 = x 2,..., X p = x p) (Рівняння лінійної регресії в загальному вигляді),
то функція y (x 1, x 2,..., x p) називається регресією величини Y за величинами X 1, X 2,..., X p, А її графік - лінією регресії Y по X 1, X 2,..., X p, Або рівнянням регресії.
62.основна задача лінійного програмування
Зада́ча ліні́йного програмува́ння — задача оптимізації з лінійною цільовою функцією та допустимою множиною обмеженою лінійними рівностями або нерівностями.
63.Графічний метод розв’язування задач лінійного програмування
Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.
Не нашли, что искали? Воспользуйтесь поиском: