Условия коллинеарности векторов

· Два вектора коллинеарные, если отношения их координат равны.

· Два вектора коллинеарные, если их векторное произведение равно нулю.

Условия компланарности векторов

· Три вектора компланарны если их смешанное произведение равно нулю.

· Три вектора компланарны если они линейно зависимы.

·

15.Скалярним добутком двох векторів a і b буде скалярна величина, яка дорівнює сумі попарного добутку відповідних координат векторів a и b.

Скалярним добутком двох векторів

a и b буде скалярна величина, яка дорівнює добутку модулів цих векторів помноженому на косинус кута між ними.

Властивість. Якщо скалярний добуток двох не нульових векторів дорівнює нулю, то ці вектори ортогональні.

Так у випадку плоскої задачі скалярний добуток векторів

a = {a_x; a_y} и b = {b_x; b_y} знаходиться за формулою a · b = a_x · b_x + a_y · b_y

Приклад 1. Знайти скалярний добуток векторів a = {1; 2} і b = {4; 8}.
Розв'язок a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20

Так у випадку просторової задачі скалярний добуток векторів a = {a_x; a_y; a_z} і b = {b_x; b_y; b_z}

знаходиться за формулою

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Приклад 1. Знайти скалярний добуток векторів a = {1; 2; -5} и b = {4;8;1}.
Розв'язок a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 - 5 = 15

Кутом між двома векторами, відкладеними від однієї точки, називається найкоротший кут, на який потрібно повернути один з векторів навколо свого початку до положення співнаправленості з іншим вектором.

Косинус кута між векторами дорівнює скалярному добутку векторів, поділеному на добуток модулів векторів.

Формула обрахунку кута між векторами

cos α = a·b/|a|·|b|

Умова паралельності

Якщо прямі паралельні, то їх напрямлені вектори коленіарні, отже їх координати будуть пропорційні

S1 = {m1;n1;p1 }

S2= {m2;n2; p2 }

m1/m2=n1/n2=p1/p2

Умова перпендикулярності

Якщо прямі взаємно перпендикулярні, то їх напрямлені вектори токож будуть взаємно перпендикулярні

Їх скалярний добуток = 0

S1*S2=0(векторы)

M1*m2+n1*n2+p1*p2=0

Умова паралельності і взаємно перпендикулярні в просторі необхідна та достатня.

16.Векторний добуток двох векторів a = {x₁; y₁; z₁} і b = {x₂; y₂; z₂} в декартовій системі координат - це вектор значення якого можна знайти за наступними формулами:

Властивість 1. Модуль векторного добутку двох векторів a і b дорівнює площині паралелограма побудованого на цих векторах. Властивість 2. Якщо векторний добуток двох векторів a и b дорівнює нулю то вектори колінеарні.

17. Мішаний добуток векторів — це скалярний добуток вектора a на векторний добуток векторів b і c. Мішаний добуток векторів дорівнює визначнику матриці, побудованої з цих векторів.

Властивість 1. Модуль мішаного добутку трьох векторів дорівнює об'єму паралелепіпеда, утвореного цими векторами.

Властивість2.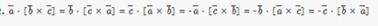

Властивість 3. Якщо мішаний добуток трьох не нульових векторів дорівнює нулю, то ці вектори компланарні.

19.Неповні загальні рівняння площини

Ax+By+Cz =0 де A,B,C і D – постійні, причому A,B,C одночасно дорівнюють нулю в векторної формі (r,N)+D = 0, де r – радіус – вектор точки M (x,y,z). Вектор N = (A,B,C) перпендикулярний до площини (нормальний вектор). Нормальна конуси вектора N:

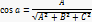
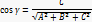
Якщо один з коефіциєнтів в рівнянні площини дорівнює нулю, рівняння називається не повним. При D=0 площину проходить через початок координат, при A=0 (або B=0, C=0) Паралельна осі Ox (Відповідно Oy або Oz.). При A=B=0 (A=C=0, або B=C=0) Плозина паралельна площині Oxy (віповідно Oxz або Oyz)

20.Кут між площинами. Перпендикуляні площини.

Кутом між двома площинами, що перетиняються, називається найменша з величин двогранних кутів, утворених цими площинами.

Площина 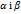між якими дорівнює 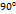, називаються перпендикулярними 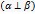. Якщо дві площини паралельні, то кут між ними вважається рівним 0.

Площина , що проходить через перпендикуляр p до другої площини 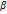. Якщо дві площини 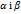взаємно перпендикулярні, то прама р, проведена в одній з цих площин перпендикулярно до їх лінії перетину, перпендикулярна і до другої площини.

Якщо – дві взаємно перпендикулятні площини і з точки А площини опущений перпендикуляр р на площину , то він лежить у площині .

21.Канонічне і параметричне рівняння прямої в просторі

Розглянемо довільну т. М (x;y;z) яка лежить на прямій, утворює вектор 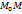та знайдемо його координати

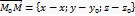
Оскільки вектор 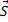і 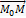колінеарні то координати їх пропорційні: 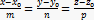– канонічне рівняння прямої в просторі.

В канонічному рівняні бічимо, що з дроби рівні між собою, запишемо, що вони рівні деякому параметру t.

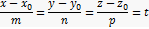
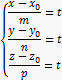
– параметричні, рівняня прямої в просторі

22.Кут між двома прямими у просторі

Нехай 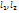задані канонічними рівняня прямих

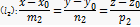
Кут між прямими 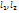вимір їх кутом між напрямами вектора.

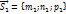
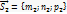
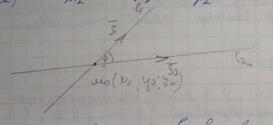
Якщо прямі 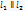то їх напрямлені вектори будуть колонарні, отже їх координати будуть коопераційні

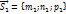
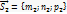
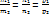– умова паралельності прямих в просторі.

Якщо пряиі то їх напрями вектора та 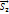також будуть взаємно перпендикулярними. Скалярний нобуток взаємний 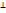векторів = D.

=0 – умова прямих в просторі.

Умов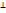а та прямих в просторі необхідна та достатня.

23.кут між прямою іплощиною

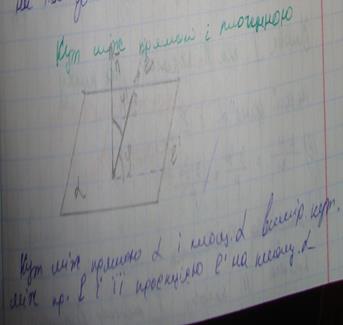
24.Означення функції. Змінна — математична велична, значення якої може змінюватися в межах певної задачі. Цим змінна відрізняється від константи.Змінна може не тільки набувати певних значень, але й визначати сенс символічних конструкцій.

Наприклад,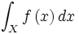

тут Х — область інтегрування, f — функція, визначена на цій області, x — аргумент функції (власне змінна в її природньому значенні), dx — безмежно малий приріст аргумента.

Постійна величина а називається границею змінної величини х, якщо абсолютна величина різниці х - а є ве­личиною нескінченно малою, тобто |х - а| < ε.Якщо число а є границею змінної х, то кажуть, що х прямує до границі а і позначають так: lim х = а або х→ а. Змінна величина х називається нескінченно ве­ликою, якщо а процесі її зміни наступиш такий момент, почи­наюча з якого абсолютна величина х стає і залишається більше будь-якого, скільки завгодно великого, наперед заданого додат­ного числа N, тобто 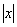>N.

25. Границя функції.геометричні зображення. Границі функції з ліва та права

Означення. Якщо кожному елементу x з області визначення D за деяким правилом поставлено у відповідність один і тільки один елемент y з області значень E, то говорять, що задано функцію y=f ( x ).

26. теореми про арифметичні властивості границь

Не нашли, что искали? Воспользуйтесь поиском: