ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ КРИВАЯ ВТОРОГО ПОРЯДКА

Общее уравнение второго порядка с двумя переменными имеет вид

А х ² + В ху + С у ² + D x + Е у + F = 0, A² + В² + С² =/= 0. (2)

Возникает естественный вопрос, что представляет собой множество точек плоскости, координаты которых удовлетворяют уравнению (2)? Другими словами, какие множества точек плоскости могут задаваться этим уравнением?

Покажем, что существует 8 различных типов таких множеств.

1) Положив в уравнении (2)

А = ¹/ _a 2, С = ¹/ _b 2, F = — l, B = D = E = 0,

получим

Итак, уравнение (2) может быть уравнением эллипса.

2) Положив в уравнении (2)

А = ¹/ _a 2, С = — ¹/ _b 2, F = — l, B = D = E = 0,

получим

Следовательно, уравнение (2) может быть уравнением гиперболы.

3) Если в уравнении (2) положить

C = l, D = — 2 p, A = В = E = F = 0,

то получим

у ² = 2 рх.

Уравнение (2) может быть уравнением параболы.

4) Если в уравнении (2) выбрать коэффициенты следующим образом:

А = а ², C = — b ², B = D = E = F = 0,

то оно примет вид

а ² х ² — b ² у ² = 0.

Так как а ² х ² — b ² у ² = (ах — by) (ах + by), то это уравнение является уравнением двух прямых:

ах — by = 0 и ах + by = 0.

Таким образом, уравнением (2) может задаваться пара пересекающихся прямых.

5) Взяв в уравнении (2)

C = l, F = — а ², A = B = D = E = 0,

получим

у ² — а ² = 0,

т. е. уравнение двух прямых у = а и у = —а.

Следовательно, уравнение (2) может быть уравнением двух параллельных прямых.

6) Положив в уравнении (2)

С = 1, A = B = D = E = F = 0,

получим

у ² = 0.

Такое уравнение принято считать уравнением пары совпавших прямых, так как из него следует, что у • у = 0 и, приравнивая каждый множитель нулю, получаем у = 0 и у = 0. Итак, уравнением (2) может быть задача пара совпавших прямых.

7) Если в уравнении (2) возьмем

А = а ², С = b ², B = D = E = F = 0,

то получим

а ² х ² + b ² у ² = 0.

Этому уравнению удовлетворяют координаты только одной точки плоскости, а именно точки (0; 0).

Отсюда следует, что уравнение (2) может задавать точку.

8) Положив в уравнении (2)

А = ¹/ _a 2, С = ¹/ _b 2, F = l, B = D = E = 0,

получим

Этому уравнению не удовлетворяют координаты ни одной точки плоскости. То же получится и в случае, когда

C = l, F = а ² =/= 0, A = B = D = E = 0.

На плоскости нет точек, координаты которых удовлетворяют уравнению

y ² + а ² = 0.

Таким образом, уравнение (2) может быть уравнением пустого множества.

Мы показали, что уравнение (2) может быть уравнением 1) эллипса, 2) гиперболы, 3) параболы, 4) пары пересекающихся прямых, 5) пары параллельных прямых, 6) пары совпавших прямых, 7) точки, 8) пустого множества.

ЭЛИПС

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами и , расстояние между ними - через 2с. По определению эллипса или .

Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид

(1)

где ; очевидно, . Уравнение вида (1) называется каноническим уравнением эллипса.

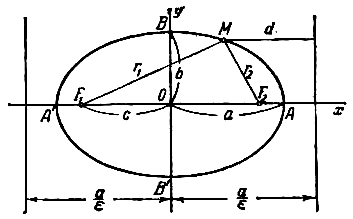
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.

Число

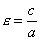
где а - большая полуось, называется эксцентриситетом эллипса. Очевидно, 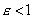(для окружности 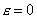). Если М(x; y) - произвольная точка эллипса, то отрезки и (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам

, .

Если эллипс определен уравнением (1) и , то прямые

,

(рис.) называются директрисами эллипса (если , то директрисы определяются уравнениями , .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:

Если две плоскости и образуют острый угол , то проекциейй на плоскость окружности радиуса a, лежащей на плоскости , является эллипс с большой полуосью а; малая полуось b этого эллипса определяется по формуле

(рис.).

Если круглый цилиндр имеет в качестве направляющей окружность радиуса b, то в сечении этого цилиндра плоскостью, наклоненной к оси цилиндра под острым углом , будет эллипс, малая полуось которого рвна b; большая полуось а этого эллипса определяется по формуле

(рис.).

ГИПЕРБОЛА

Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами и , расстояние между ними - через 2с. По определению гиперболы , или .

Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

(1)

где . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.

Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть

,

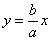Уравнение

(2)

определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.

Две гиперболы, которые определяются уравнениями

,

в одной и той же системе координат, называются сопряженными.

Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид

или

Число

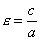
где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы . Если М(x; y) - произвольная точка гиперболы, то отрезки и (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам

, ,

фокальные радиусы точек левой ветви - по формулам

, .

Если гипербола задана уравнением (1), то прямые, определяемые уравнениями

, ,

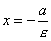называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями

, .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:

.

ПАРАБОЛА

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

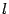Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора 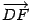. Ось проведем перпендикулярно оси (рис. 12.15).

Рис.12.15.

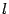Теорема 12.4 Пусть расстояние между фокусом и директрисой параболы равно . Тогда в выбранной системе координат парабола имеет уравнение

(12.10)

Доказательство. В выбранной системе координат фокусом параболы служит точка , а директриса имеет уравнение (рис. 12.15).

Пусть 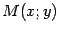-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим

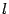Расстоянием от точки до директрисы служит длина перпендикуляра , опущенного на директрису из точки . Из рисунка 12.15 очевидно, что 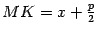. Тогда по определению параболы , то есть

Возведем обе части последнего уравнения в квадрат:

откуда

После приведения подобных членов получим уравнение (12.10).

Уравнение (12.10) называется каноническим уравнением параболы.

Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .

Доказательство. Проводится так же, как и доказательство (предложения 12.1).

Точка пересечения оси симметрии с параболой называется вершиной параболы.

Если переобозначить переменные , , то уравнение (12.10) можно записать в виде

который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).

Рис.12.16.Парабола

Пример 12.6 Постройте параболу . Найдите ее фокус и директрису.

Решение. Уравнение является каноническим уравнением параболы, , . Осью параболы служит ось , вершина находится в начале координат, ветви параболы направлены вдоль оси . Для построения найдем несколько точек параболы. Для этого придаем значения переменному и находим значения . Возьмем точки , , . Учитывая симметрию относительно оси , рисуем кривую (рис. 12.17)

Рис.12.17.Парабола, заданная уравнением

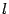Фокус лежит на оси на расстоянии от вершины, то есть имеет координаты . Директриса имеет уравнение , то есть .

Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.

Предложение 12.5 Пусть -- фокус параболы, -- произвольная точка параболы, 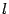-- луч с началом в точке параллельный оси параболы. Тогда нормаль к параболе в точке делит угол, образованный отрезком 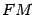и лучом 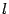, пополам.

Рис.12.18.Отражение светового луча от параболы

Это свойство означает, что луч света, вышедший из фокуса , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.

Не нашли, что искали? Воспользуйтесь поиском: