Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0

при условии, что не имеет место равенство

ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКА

Определение матрицы. Определители второго и третьего порядков, их основные свойства. Миноры и алгебраические дополнения, разложение определителя по строке (столбцу). Методы вычисления определителей. Понятие об определителе n-го порядка.

Определение 1.1. Матрицей называется прямоугольная таблица чисел.

Обозначения: А – матрица, 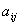- элемент матрицы, номер строки, в которой стоит данный элемент, номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Определение 1.2. Числа m и n называются размерностями матрицы.

Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.

Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

.

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

Примеры.

1. 2.

Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:

Примеры.

1.

2.

Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a`_ij = a_ji.

Не нашли, что искали? Воспользуйтесь поиском: