ОПЕРАЦИИ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы и одинакового размера m на n называются равными, если , i = 1,2,…,m, j=1,2,…,n.

Если матрицы A и B равны, то будем писать A=B.

Линейные операции. Суммой двух матриц A и B размера m на n называется матрица C размера m на n, элементы которой определяются равенством

Сумму матриц A и B будем обозначать C=A+B.

Матрица 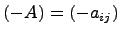называется противоположной к матрице .

Теорема 2.1 Операция сложения матриц обладает следующими свойствами: для любых матриц и нулевой матрицы

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.

Разностью матриц и называется матрица A+(-B).

Не нашли, что искали? Воспользуйтесь поиском: