Если определитель матрицы равен нулю, то обратная к ней не существует.

Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.

Определение 14.9 Квадратную матрицу 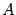назовем вырожденной или особенной матрицей, если 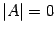, и невырожденной или неособенной матрицей, если .

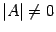Предложение 14.21 Если обратная матрица существует, то она единственна.

Доказательство. Пусть две матрицы и 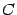являются обратными для матрицы 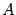. Тогда

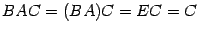и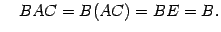

Следовательно, .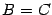

Предложение 14.22 Если квадратная матрица 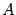является невырожденной, то обратная для нее существует и

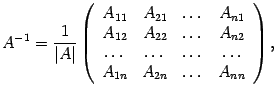
(14.14)

где 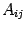-- алгебраические дополнения к элементам .

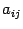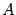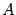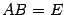Доказательство. Так как для невырожденной матрицы правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что 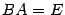. Докажем первое из этих равенств, второе доказывается аналогично.

Пусть 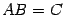. Найдем элементы матрицы 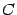, учитывая, что :

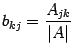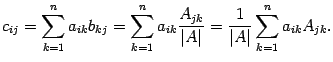
Если 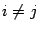, то по предложению 14.17 сумма справа равна нулю, то есть 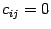при .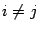

Если 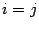, то

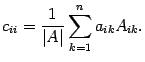
Сумма справа представляет собой разложение определителя матрицы 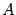по 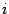-ой строке (предложение 14.16). Таким образом,

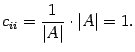
Итак, в матрице 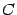диагональные элементы равны 1, а остальные равны нулю, то есть .

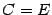Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему.

Теорема 14.1 Обратная матрица для квадратной матрицы 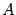существует тогда и только тогда, когда матрица 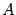-- невырожденная, обратная матрица единственна, и справедлива формула (14.14).

Замечание 14.12 Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй -- номер строки, в которые нужно записать вычисленное алгебраическое дополнение.

Пример 14.7 Найдите обратную матрицу для матрицы .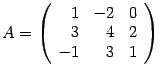

Решение. Находим определитель

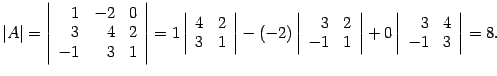
Так как 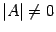, то матрица 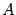-- невырожденная, и обратная для нее существует.

Находим алгебраические дополнения:

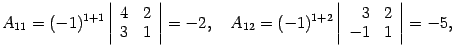
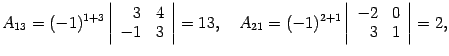
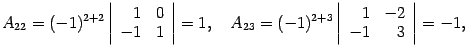
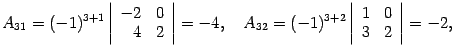
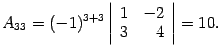
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй -- строке:

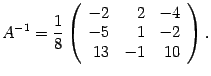
(14.15)

Полученная матрица и служит ответом к задаче.

Замечание 14.13 В предыдущем примере было бы точнее ответ записать так:

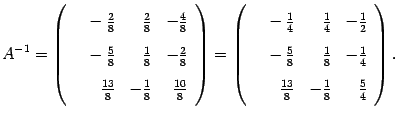
(14.16)

Однако запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (14.15) предпочтительнее, если элементы матриц -- целые числа. И наоборот, если элементы матрицы 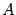-- десятичные дроби, то обратную матрицу лучше записать без множителя 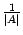впереди.

Замечание 14.14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.

Пример 14.8 Найдите обратную матрицу для матрицы .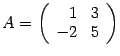

Решение.

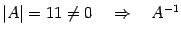-- существует.

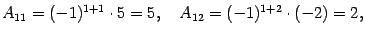
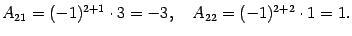
Ответ: .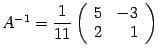

Нахождение обратной матрицы по формуле (14.14) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.

Не нашли, что искали? Воспользуйтесь поиском: