Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.

Как бы мы поступили в школе, если бы получили задание найти решение системы уравнений .

Некоторые сделали бы так.

Заметим, что прибавив к левой части второго уравнения левую часть первого, а к правой части - правую, можно избавиться от неизвестных переменных x₂ и x₃ и сразу найти x₁:

Подставляем найденное значение x₁ = 1 в первое и третье уравнение системы:

Если умножить обе части третьего уравнения системы на - 1 и прибавить их к соответствующим частям первого уравнения, то мы избавимся от неизвестной переменной x₃ и сможем найти x₂:

Подставляем полученное значение x₂ = 2 в третье уравнение и находим оставшуюся неизвестную переменную x₃:

Другие поступили бы иначе.

Разрешим первое уравнение системы относительно неизвестной переменной x₁ и подставим полученное выражение во второе и третье уравнение системы, чтобы исключить из них эту переменную:

Теперь разрешим второе уравнение системы относительно x₂ и подставим полученный результат в третье уравнение, чтобы исключить из него неизвестную переменную x₂:

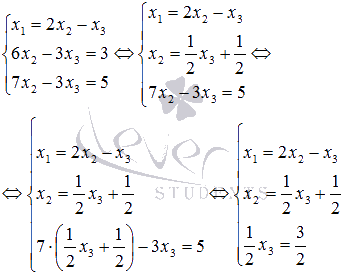
Из третьего уравнения системы видно, что x₃ = 3. Из второго уравнения находим , а из первого уравнения получаем .

Знакомые способы решения, не правда ли?

Самое интересное здесь то, что второй способ решения по сути и есть метод последовательного исключения неизвестных, то есть, метод Гаусса. Когда мы выражали неизвестные переменные (сначала x₁, на следующем этапе x₂) и подставляли их в остальные уравнения системы, мы тем самым исключали их. Исключение мы проводили до того момента, пока в последнем уравнении не осталась одна единственная неизвестная переменная. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса.

Следует заметить, что когда мы выражаем x₁ через x₂ и x₃ в первом уравнении, а затем подставляем полученное выражение во второе и третье уравнения, то к такому же результату приводят следующие действия:

• к левой и правой частям второго уравнения прибавляем соответствующие части первого уравнения, умноженные на ,

• к левой и правой частям третьего уравнения прибавляем соответствующие части первого уравнения, умноженные на .

Действительно, такая процедура также позволяет исключить неизвестную переменную x₁ из второго и третьего уравнений системы:

Нюансы с исключением неизвестных переменных по методу Гаусса возникают тогда, когда уравнения системы не содержат некоторых переменных.

Например, в СЛАУ в первом уравнении отсутствует неизвестная переменная x₁ (иными словами, коэффициент перед ней равен нулю). Поэтому мы не можем разрешить первое уравнение системы относительно x₁, чтобы исключить эту неизвестную переменную из остальных уравнений. Выходом из этой ситуации является перестановка местами уравнений системы. Так как мы рассматриваем системы линейных уравнений, определители основных матриц которых отличны от нуля, то всегда существует уравнение, в котором присутствует нужная нам переменная, и мы это уравнение можем переставить на нужную нам позицию. Для нашего примера достаточно поменять местами первое и второе уравнения системы , дальше можно разрешить первое уравнение относительно x₁ и исключить ее из остальных уравнений системы (хотя во втором уравнении x₁ уже отсутствует).

Надеемся, что суть Вы уловили.

Опишем алгоритм метода Гаусса.

Пусть нам требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида , и пусть определитель ее основной матрицы отличен от нуля.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид

где , а .

К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

Будем считать, что (в противном случае мы переставим местами вторую строку с k-ой, где ). Приступаем к исключению неизвестной переменной x₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

где , а . Таким образом, переменная x₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

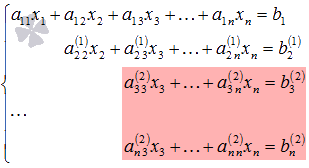
Так продолжаем прямой ход метода Гаусса пока система не примет вид

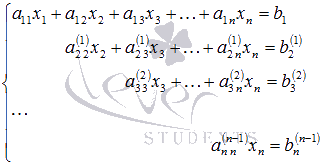
С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как , с помощью полученного значения x_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Разберем алгоритм на примере.

Пример.

Найдите решение системы уравнений методом Гаусса.

Решение.

Коэффициент a_{1 1} отличен от нуля, так что приступим к прямому ходу метода Гаусса, то есть, к исключению неизвестной переменной x₁ из всех уравнений системы, кроме первого. Для этого к левой и правой частям второго, третьего и четвертого уравнения прибавим левую и правую части первого уравнения, умноженные соответственно на , и :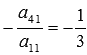

Неизвестную переменную x₁ исключили, переходим к исключению x₂. К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и :

Для завершения прямого хода метода Гаусса нам осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Прибавим к левой и правой частям четвертого уравнения соответственно левую и правую часть третьего уравнения, умноженную на :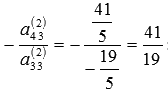

Можно начинать обратный ход метода Гаусса.

Из последнего уравнения имеем ,

из третьего уравнения получаем ,

из второго ,

из первого .

Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно.

Ответ: .

А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи.

Расширенная матрица системы имеет вид . Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы.

Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь.

Преобразуем матрицу так, чтобы все элементы в первом столбце, начиная со второго, стали нулевыми. Для этого к элементам второй, третьей и четвертой строк прибавим соответствующие элементы первой строки умноженные на , и на 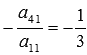соответственно:

Далее полученную матрицу преобразуем так, чтобы во втором столбце все элементы, начиная с третьего стали нулевыми. Это будет соответствовать исключению неизвестной переменной x₂. Для этого к элементам третьей и четвертой строк прибавим соответствующие элементы первой строки матрицы, умноженные соответственно на и :

Осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на :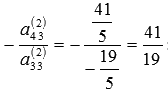

Следует отметить, что эта матрица соответствует системе линейных уравнений

которая была получена ранее после прямого хода.

Пришло время обратного хода. В матричной форме записи обратный ход метода Гаусса предполагает такое преобразование полученной матрицы, чтобы матрица, отмеченная на рисунке

стала диагональной, то есть, приняла вид

где - некоторые числа.

Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой.

Прибавим к элементам третьей, второй и первой строк соответствующие элементы последней строки, умноженные на , на и на соответственно:

Теперь прибавим к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на и на соответственно:

На последнем шаге обратного хода метода Гаусса к элементам первой строки прибавляем соответствующие элементы второй строки, умноженные на :

Полученная матрица соответствует системе уравнений , откуда находим неизвестные переменные.

Ответ: .

РАНГ МАТРИЦЫ

Ранг матрицы представляет собой важную числовую характеристику. Наиболее характерной задачей, требующей нахождения ранга матрицы, является проверка совместности системы линейных алгебраических уравнений. В этой статье мы дадим понятие ранга матрицы и рассмотрим методы его нахождения. Для лучшего усвоения материала подробно разберем решения нескольких примеров.

Возьмем матрицу А порядка 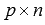. Пусть k – некоторое натуральное число, не превосходящее наименьшего из чисел m и n, то есть, .

Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка , составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется.

Другими словами, если в матрице А вычеркнуть (p – k) строк и (n – k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы есть минор порядка k матрицы А.

Разберемся с определением минора матрицы на примере.

Рассмотрим матрицу .

Запишем несколько миноров первого порядка этой матрицы. К примеру, если мы выберем третью строку и второй столбец матрицы А, то нашему выбору соответствует минор первого порядка . Иными словами, для получения этого минора мы вычеркнули первую и вторую строки, а также первый, третий и четвертый столбцы из матрицы А, а из оставшегося элемента составили определитель. Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор .

Проиллюстрируем процедуру получения рассмотренных миноров первого порядка

и .

Таким образом, минорами первого порядка матрицы являются сами элементы матрицы.

Покажем несколько миноров второго порядка. Выбираем две строки и два столбца. К примеру, возьмем первую и вторую строки и третий и четвертый столбец. При таком выборе имеем минор второго порядка . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов.

Другим минором второго порядка матрицы А является .

Проиллюстрируем построение этих миноров второго порядка

и .

Аналогично могут быть найдены миноры третьего порядка матрицы А. Так как в матрице А всего три строки, то выбираем их все. Если к этим строкам выбрать три первых столбца, то получим минор третьего порядка

Он также может быть построен вычеркиванием последнего столбца матрицы А.

Другим минором третьего порядка является

получающийся вычеркиванием третьего столбца матрицы А.

Вот рисунок, показывающий построение этих миноров третьего порядка

и .

Для данной матрицы А миноров порядка выше третьего не существует, так как .

Сколько же существует миноров k-ого порядка матрицы А порядка ?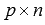

Число миноров порядка k может быть вычислено как , где и - число сочетаний из p по k и из n по k соответственно.

Как же построить все миноры порядка k матрицы А порядка p на n?

Нам потребуется множество номеров строк матрицы 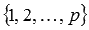и множество номеров столбцов . Записываем все сочетания из p элементов по k (они будут соответствовать выбираемым строкам матрицы А при построении минора порядка k). К каждому сочетанию номеров строк последовательно добавляем все сочетания из n элементов по k номеров столбцов. Эти наборы сочетаний номеров строк и номеров столбцов матрицы А помогут составить все миноры порядка k.

Разберем на примере.

Пример.

Найдите все миноры второго порядка матрицы .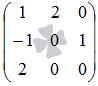

Решение.

Так как порядок исходной матрицы равен 3 на 3, то всего миноров второго порядка будет .

Запишем все сочетания из 3 по 2 номеров строк матрицы А: 1, 2; 1, 3 и 2, 3. Все сочетания из 3 по 2 номеров столбцов есть 1, 2; 1, 3 и 2, 3.

Возьмем первую и вторую строки матрицы А. Выбрав к этим строкам первый и второй столбцы, первый и третий столбцы, второй и третий столбцы, получим соответственно миноры

Для первой и третьей строк при аналогичном выборе столбцов имеем

Осталось ко второй и третьей строкам добавить первый и второй, первый и третий, второй и третий столбцы:

Итак, все девять миноров второго порядка матрицы А найдены.

Сейчас можно переходить к определению ранга матрицы.

Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля.

Ранг матрицы А обозначают как Rank(A). Можно также встретить обозначения Rg(A) или Rang(A).

Из определений ранга матрицы и минора матрицы можно заключить, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы не меньше единицы.

ОБРАТИТЕ ВНИМАНИЕ: при проведении элементарных преобразований не допускаются приближенные вычисления!

Рассмотрим еще один пример.

Пример.

Методом элементарных преобразований найдите ранг матрицы .

Решение.

Поменяем местами первую и вторую строки матрицы А, так как элемент a_{1 1} равен нулю, а элемент a_{2 1} отличен от нуля:

В полученной матрице элемент равен единице, поэтому не нужно производить умножение элементов первой строки на . Сделаем все элементы первого столбца, кроме первого, нулевыми:

Так первый столбец преобразован к нужному виду.

Элемент 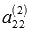в полученной матрице отличен от нуля. Умножим элементы второй строки на :

Второй столбец полученной матрицы имеет нужный вид, так как элемент 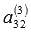уже равен нулю.

Так как , а 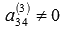, то поменяем местами третий и четвертый столбцы:

Умножим третью строку полученной матрицы на :

На этом заканчиваем преобразования. Получаем Rank(A⁽⁵⁾) = 3, следовательно, Rank(A) = 3.

Ответ: ранг исходной матрицы равен трем.

Подведем итог.

Мы разобрали понятие ранга матрицы и рассмотрели три способа его нахождения:

• по определению методом перебора всех миноров;

• методом окаймляющих миноров;

• методом элементарных преобразований.

Целесообразно всегда использовать метод элементарных преобразований при нахождении ранга матрицы, так как он приводит к результату при меньшем объеме вычислений, по сравнению с методом окаймляющих миноров, и тем более в сравнении с методом перебора всех миноров матрицы.

Не нашли, что искали? Воспользуйтесь поиском: