
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Собственные значения и собственные векторы матрицы. Найти собственные значения и собственные векторы матрицы .Решение: Составим характеристическое уравнение

Или.Раскроем скобки и приведём подобные слагаемые или.Отсюда или.Вынесем общий множитель за скобки. Тогда получим уравнение
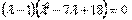
Произведение равно нулю, когда один из сомножителей равен нулю. Получаем совокупность уравнений
 Второе уравнение совокупности - квадратное уравнение с отрицательным дискриминантом
Второе уравнение совокупности - квадратное уравнение с отрицательным дискриминантом 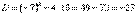
Следовательно оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень, а матрица только одно собственное значение. Найдём собственный вектор, принадлежащий этому собственному значению, решая уравнение
 Расписывая по компонентам и подставляя
Расписывая по компонентам и подставляя 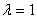 , получим систему из трёх уравнений с тремя неизвестными:
, получим систему из трёх уравнений с тремя неизвестными:
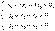 Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде:
Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде:
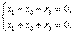 Сложим оба уранения, а затем из второго вычтем первое. Получим
Сложим оба уранения, а затем из второго вычтем первое. Получим 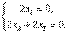
Отсюда 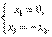 и мы имеем собственный вектор x=
и мы имеем собственный вектор x=
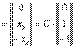
3 0.линейная модель торговли. Процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы. Будем полагать, что бюджеты n стран, которые обозначим соответственно 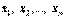 , расходуются на покупку товаров. Пусть
, расходуются на покупку товаров. Пусть 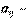 доля бюджета
доля бюджета 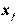 , которую j –я страна тратит на закупку товаров у
, которую j –я страна тратит на закупку товаров у 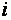 -й страны. Введём матрицу коэффициентов
-й страны. Введём матрицу коэффициентов 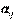 :
: 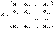 . Тогда, если весь бюджет расходуется только на закупки внутри страны и вне её (это можно трактовать как торговый бюджет), справедливо равенство
. Тогда, если весь бюджет расходуется только на закупки внутри страны и вне её (это можно трактовать как торговый бюджет), справедливо равенство 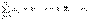 Матрица (1) со свойством (2), в силу которого сумма элементов её любого столбца равна единице, называется структурной матрицей торговли. Для
Матрица (1) со свойством (2), в силу которого сумма элементов её любого столбца равна единице, называется структурной матрицей торговли. Для  -й страны общая выручка от внутренней и внешней торговли выражается формулой
-й страны общая выручка от внутренней и внешней торговли выражается формулой 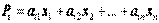 . Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны её бюджет должен быть не больше выручки от торговли, а в силу условия (2)
. Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны её бюджет должен быть не больше выручки от торговли, а в силу условия (2) 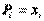 или
или 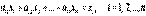 Таким образом, условия (4) принимают вид равенств:
Таким образом, условия (4) принимают вид равенств: 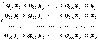 . Введём вектор бюджетов
. Введём вектор бюджетов 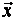 , каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:
, каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:  . Это уравнение означает, что собственный вектор структурной матрицы А, отвечает её собственному значению
. Это уравнение означает, что собственный вектор структурной матрицы А, отвечает её собственному значению 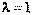 , состоит из бюджетов стран бездефицитной международной торговли.Перепишем уравнение (6) в виде, позволяющем определить
, состоит из бюджетов стран бездефицитной международной торговли.Перепишем уравнение (6) в виде, позволяющем определить 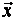 :
: 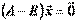 . Задача. Дана структурная матрица торговли трёх стран
. Задача. Дана структурная матрица торговли трёх стран 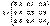 .Найти бюджеты этих стран, удовлетворяющие бездефицитной торговле, при условии, что сумма бюджетов равна
.Найти бюджеты этих стран, удовлетворяющие бездефицитной торговле, при условии, что сумма бюджетов равна 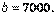 Решение: Легко видеть, что элементы матрицы А удовлетворяют условиям структурной матрице торговли. Следовательно, существует собственный вектор, соответствующий собственному значению 1.Из уравнения
Решение: Легко видеть, что элементы матрицы А удовлетворяют условиям структурной матрице торговли. Следовательно, существует собственный вектор, соответствующий собственному значению 1.Из уравнения 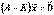 получим
получим 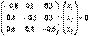 или
или 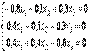 .Решим систему методом Гаусса
.Решим систему методом Гаусса 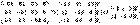 Получим систему
Получим систему 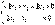 Откуда
Откуда 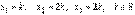 .Учитывая, что сумма
.Учитывая, что сумма 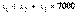 , определим величину
, определим величину 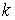 :
: 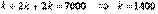 .Поэтому
.Поэтому 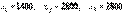 .Таким образом, искомые величины бюджетов стран при бездефицитной торговле соответственно равны:
.Таким образом, искомые величины бюджетов стран при бездефицитной торговле соответственно равны: 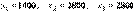 .
.
31.квадратичные формы.приведение квадратичной формык конаническому виду. Пусть 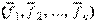 – базис линейного пространства
– базис линейного пространства 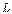 , по отношению к которому квадратичная форма представляется в виде
, по отношению к которому квадратичная форма представляется в виде 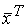 А
А 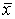
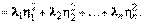 Выражение (8.2) называется каноническим видом квадратичной формы.Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, а невырожденному преобразованию координат – преобразование базиса, то вопрос о приведении квадратичной формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат. Теорема 8.2 (метод Лагранжа). Любая квадратичная форма
Выражение (8.2) называется каноническим видом квадратичной формы.Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, а невырожденному преобразованию координат – преобразование базиса, то вопрос о приведении квадратичной формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат. Теорема 8.2 (метод Лагранжа). Любая квадратичная форма 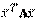 , заданная в n-мерном линейном пространстве L, с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду (8.2). Основная идея этого метода заключается в последовательном дополнении квадратного трехчлена по каждому аргументу до полного квадрата. Теорема 8.3. В евклидовом пространстве U существует такой ортонормированный базис
, заданная в n-мерном линейном пространстве L, с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду (8.2). Основная идея этого метода заключается в последовательном дополнении квадратного трехчлена по каждому аргументу до полного квадрата. Теорема 8.3. В евклидовом пространстве U существует такой ортонормированный базис 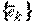 и можно указать такие вещественные числа
и можно указать такие вещественные числа 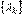 , что для любого
, что для любого 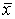 из U квадратичная форма
из U квадратичная форма 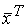 А
А 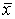 может быть представлена в виде (8.2).Для матрицы А можно указать ортонормированный базис
может быть представлена в виде (8.2).Для матрицы А можно указать ортонормированный базис 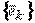 из собственных векторов матрицы А. Пусть
из собственных векторов матрицы А. Пусть 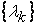 – собственные значения, отвечающие
– собственные значения, отвечающие  . Тогда
. Тогда 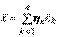 и
и 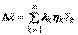 и вследствие ортонормированности базиса
и вследствие ортонормированности базиса 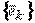
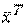 А
А 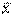
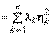 .
.
Приведение квадратичной формы к каноническому виду можно использовать для приведения к каноническому виду уравнений линий и поверхностей второго порядка.
32.определение положительной и отрицательной квад формы. 1 т. е. квадратичная форма является положительно определенной.2 т. е. квадратичная форма является отрицательно определенной.3 данная квадратичная форма не является знакоопределенной, так как она равна 0 во всех точках прямой х1 = -х2, а не только в начале системы координат.
Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их. 3. Критерий положительной и отрицательной определенности
Критерий положительной определенности (критерий Сильвестра)
Для того чтобы квадратичная форма (х) = хТАх была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть:
М1 > 0, M2 > 0, …, Mn > 0.
Критерий отрицательной определенности
Для того чтобы квадратичная форма (х) = хТАх была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного - отрицательны, то есть:
М1 < 0, M2 > 0, М3 < 0, …, (-1)n Mn > 0. При каких значениях а и в квадратичная форма будет отрицательно определенной?
(х1, х2, x3) = Решение. М1 = -1 < 0,= -а - 1 > 0 а < -1.= -ав - а - в < 0 в > -.
Ответа < -1, в > -.Пример 5. Д оказать, что квадратичная форма
(х1, х2, x3) = положительно пределена.Решение.Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А. М1 = 6 > 0, = 26 > 0, М3 = А = 162 > 0(х1, х2, x3)
33.понятие комплексного числа.геом интрприкация комплексного числа.алгебр и триганом форма записи компл числа. Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом: 1) два комплексных числа z 1 = (x 1, y 1) и z 2 = (x 2, y 2) называются равными, если x 1 = x 2 и y 1 = y 2; 2) суммой комплексных чисел z 1 и z 2 называется комплексное число z вида z = (x 1 + x 2, y 1 + y 2); 3) произведением комплексных чисел z 1 и z 2 называется комплексное число z = (x 1 x 2 - y 1 y 2, x 1 y 2 + x 2 y 1); 4) множество комплексных чисел 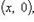
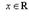 , отождествляется с множеством действительных чисел R. Эта запись называется алгебраической формой комплексного числа. Комплексное число
, отождествляется с множеством действительных чисел R. Эта запись называется алгебраической формой комплексного числа. Комплексное число 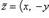
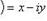 называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy. Геометрическая интерпретация комплексного числа Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой. Расстояние r точки z от нулевой точки, т. е. число
называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy. Геометрическая интерпретация комплексного числа Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой. Расстояние r точки z от нулевой точки, т. е. число 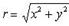
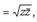 называется модулем комплексного числа z и обозначается символом | z |.Число
называется модулем комплексного числа z и обозначается символом | z |.Число 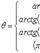
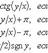
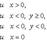 называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на
называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на 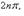
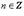 , соответствуют одному и тому же числу. В этом случае записываем
, соответствуют одному и тому же числу. В этом случае записываем 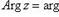
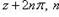
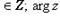 называем главным значением аргумента.Числа r и θ называют полярными координатами комплексного числа z. В этом случае z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ)называется тригонометрической формой комплексного числа.Если z 1 = (r 1 cos θ 1, r 1 sin θ 1), z 2 = (r 2 cos θ 2, r 2 sin θ 2), то z 1 z 2 = (r 1 r 2 cos(θ 1 + θ 2), r 1 r 2 sin(θ 1 + θ 2)),
называем главным значением аргумента.Числа r и θ называют полярными координатами комплексного числа z. В этом случае z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ)называется тригонометрической формой комплексного числа.Если z 1 = (r 1 cos θ 1, r 1 sin θ 1), z 2 = (r 2 cos θ 2, r 2 sin θ 2), то z 1 z 2 = (r 1 r 2 cos(θ 1 + θ 2), r 1 r 2 sin(θ 1 + θ 2)), 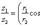
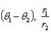
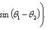 Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ).При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра. Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ).При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра. Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле 
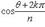
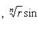
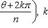
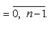
34. основные свойства компл чисел. На комплексные числа распространяются все основные законы действия над действительными числами. Они легко выводятся из определения арифметических операций. 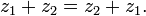
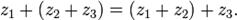
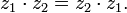
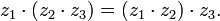
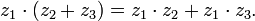
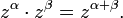
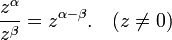
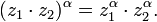
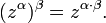
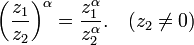
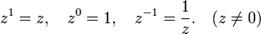 Сложение двух комплексных чисел
Сложение двух комплексных чисел 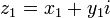 и
и 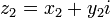 выполняется по следующему правилу:
выполняется по следующему правилу: 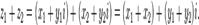 Чтобы получить правило вычитания одного комплексного числа из другого, воспользуемся определением: разностью двух комплексных чисел
Чтобы получить правило вычитания одного комплексного числа из другого, воспользуемся определением: разностью двух комплексных чисел 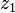 и
и 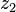 называется такое
называется такое 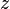 , что верно равенство:
, что верно равенство: 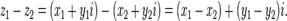 Рассмотрим теперь произведение двух комплексных чисел
Рассмотрим теперь произведение двух комплексных чисел 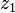 и
и 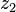 в алгебраической форме:
в алгебраической форме:
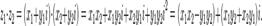
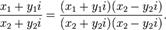
35. возвед в степень и извлеч корня… Возведение в целую степень. Прежде чем рассматривать вопрос возведения в степень произвольного комплексного числа 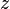 , рассмотрим какие результаты даёт возведение в степень мнимой единицы
, рассмотрим какие результаты даёт возведение в степень мнимой единицы 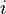 . По определению натуральной степенью
. По определению натуральной степенью 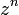 называется
называется 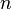 -кратное произведение числа
-кратное произведение числа 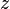 на самого себя:
на самого себя:  (Д2.36)Для
(Д2.36)Для 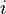 последовательно будем иметь:
последовательно будем иметь: 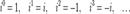 (Д2.37)Продолжая умножение, можно получить следующее обобщение:
(Д2.37)Продолжая умножение, можно получить следующее обобщение: 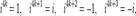 (Д2.38)где
(Д2.38)где 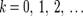 При возведение в степень числа
При возведение в степень числа 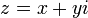 в натуральную степень
в натуральную степень 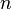 воспользуемся формулой биноманьютона:
воспользуемся формулой биноманьютона: 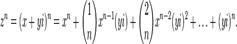 (Д2.39)Теперь, упрощая каждый моном по формулам (Д2.38) и группируя члены, содержащие и не содержащие
(Д2.39)Теперь, упрощая каждый моном по формулам (Д2.38) и группируя члены, содержащие и не содержащие 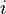 , в итоге получим некое комплексное число
, в итоге получим некое комплексное число 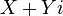 . Таким образом, натуральная степень комплексного числа, у которого действительная часть отлична от нуля, также является комплексным числом. Степень чисто мнимого числа может быть и действительным числом.Так как, по определению,
. Таким образом, натуральная степень комплексного числа, у которого действительная часть отлична от нуля, также является комплексным числом. Степень чисто мнимого числа может быть и действительным числом.Так как, по определению, 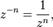 (Д2.40)то нужно сначала возвести в степень
(Д2.40)то нужно сначала возвести в степень 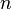 по формуле (Д2.39), а затем найти обратную величину по формуле (Д2.34).Из выше сказанного следует, что при любом целом, отличном от нуля, показателе степени, для комплексного числа общего вида мы получаем другое комплексное число. Если возводить в целую степень чисто мнимое число, то в результате может получиться либо действительное, либо чисто мнимое число.Вопрос извлечения корней из комплексных чисел мы рассмотрим на примере извлечения квадратного корня. В дальнейшем будет более подробно показано, что извлечение корня для комплексных чисел всегда осуществимо и многозначно.Итак, по определению, квадратным корнем из комплексного числа
по формуле (Д2.39), а затем найти обратную величину по формуле (Д2.34).Из выше сказанного следует, что при любом целом, отличном от нуля, показателе степени, для комплексного числа общего вида мы получаем другое комплексное число. Если возводить в целую степень чисто мнимое число, то в результате может получиться либо действительное, либо чисто мнимое число.Вопрос извлечения корней из комплексных чисел мы рассмотрим на примере извлечения квадратного корня. В дальнейшем будет более подробно показано, что извлечение корня для комплексных чисел всегда осуществимо и многозначно.Итак, по определению, квадратным корнем из комплексного числа 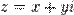 называется такое комплексное число
называется такое комплексное число 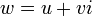 , что имеет место равенство
, что имеет место равенство 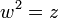 , то есть:
, то есть: 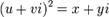 (Д2.41)или, раскрывая скобки,
(Д2.41)или, раскрывая скобки, 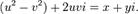 (Д2.42)Сравнивая действительные и мнимые части комплексных чисел, приходим к системе уравнений:
(Д2.42)Сравнивая действительные и мнимые части комплексных чисел, приходим к системе уравнений: 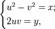 (Д2.43)решая которую будем иметь:
(Д2.43)решая которую будем иметь: 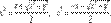 (Д2.44)Выражения
(Д2.44)Выражения 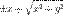 неотрицательны при любых действительных
неотрицательны при любых действительных 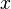 и
и 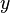 , следовательно, числа
, следовательно, числа 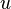 и
и 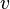 всегда можно найти из (Д2.44); при этом они будут действительны. При извлечении арифметических корней в (Д2.44) необходимо учитывать знаки таким образом, чтобы выполнялось соотношение
всегда можно найти из (Д2.44); при этом они будут действительны. При извлечении арифметических корней в (Д2.44) необходимо учитывать знаки таким образом, чтобы выполнялось соотношение 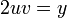 , которое задаёт два различных набора действительных чисел. Соответственно, извлечение корня из
, которое задаёт два различных набора действительных чисел. Соответственно, извлечение корня из 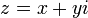 даёт два комплексных числа
даёт два комплексных числа 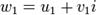 и
и  .
.
36. множества. Операции над ними. Множество – совокупность некоторых объектов. Примерами множеств являются множества чисел, множества точек прямой, множество линий и др. Каждое отдельное множество задается правилом или законом, позволяющим судить, принадлежит объект данному множеству или нет. Множества обозначаются прописными буквами латинского или готического алфавита: A, B,...,M, K,.... Если множество A состоит из элементов a,b,c,..., это обозначается с помощью фигурных скобок: A={a,b,c,...,}. Если a есть элемент множества A, то это записывают следующим образом: a Î A. Если же a не является элементом множества A, то пишут a Ï A. Одним из важных множеств является множество N всех натуральных чисел N={1,2,3,...,}. Существует также специальное, так называемое пустое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом Æ. соотношения xÎ A и xÎ B равносильны. Операции над множествами.Объединение.
(рис. 1) C=A È B: = { x:x Î A или x Î B }  Пример 2. Решить неравенство | 2 x+ 1 | > 3.Из данного неравенства следует либо неравенство 2 x+ 1>3в случае, когда 2 x+ 1³ 0, тогда x> 1, либо неравенство 2 x+ 1<-3,в случае, когда 2 x+ 1<0, тогда x<- 2.Множеством решений исходного неравенства является объединение найденных промежутков решения (-¥,-2)È (1,+¥). Пример. A = {1; 3; 5; 7 ;...; 2 n- 1 ;.... } — нечетные числа B = {2; 4; 6; 8 ;....; 2 n;... } — четные числа A È B = {1; 2; 3 ;...; n;...... } — натуральный ряд Пересечение.(рис. 2) C=A Ç B:= { x: x Î A и x Î B }
Пример 2. Решить неравенство | 2 x+ 1 | > 3.Из данного неравенства следует либо неравенство 2 x+ 1>3в случае, когда 2 x+ 1³ 0, тогда x> 1, либо неравенство 2 x+ 1<-3,в случае, когда 2 x+ 1<0, тогда x<- 2.Множеством решений исходного неравенства является объединение найденных промежутков решения (-¥,-2)È (1,+¥). Пример. A = {1; 3; 5; 7 ;...; 2 n- 1 ;.... } — нечетные числа B = {2; 4; 6; 8 ;....; 2 n;... } — четные числа A È B = {1; 2; 3 ;...; n;...... } — натуральный ряд Пересечение.(рис. 2) C=A Ç B:= { x: x Î A и x Î B } 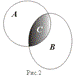
Пример 4. A={2,4,...,2n,...}, B={3,6,9,...,3n,...}. Тогда C=AÇ B={6,12,...,6n,...}. Вычитание. (рис. 3) A \ B: = { x:x Î A и x Ï B } 
1. Дополнение. (рис.4) Пусть U — универсальное множество (все остальные множества принадлежат U) A = CA: = { x:x Î U и x Ï A } = U \ A 
2. Симметрическая разность.
(рис. 5)
A D B:= (A \ B) È (B \ A) = (A È B) \ (A Ç B)
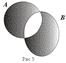
37.основные элементарные функции. Линейная функция подробно рассматривалась в разделе "Аналитическая геометрия". Степенная функция определяется соотношением y = xn, n ≠ 0. При натуральных значениях n эта функция определена на всей числовой прямой, т. е. х 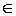 R. При четном показателе степени степенная функция является четной и y принимает положительные значения. Ее графиками служат параболы соответственно второго, четвертого и т.д. порядков, При нечетном показателе функция является нечетной и принимает значения y
R. При четном показателе степени степенная функция является четной и y принимает положительные значения. Ее графиками служат параболы соответственно второго, четвертого и т.д. порядков, При нечетном показателе функция является нечетной и принимает значения y 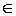 (− ∞, + ∞). Ее графиками служат параболы третьего, пятого и т. д. порядков
(− ∞, + ∞). Ее графиками служат параболы третьего, пятого и т. д. порядков
П о к а з а т е л ь н а я функция y = ax, ( a ≠ 1, a > 0). Область ее определения x 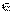 (- ∞, + ∞), множество значений y
(- ∞, + ∞), множество значений y 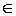 (0, + ∞). Если a > 1, то функция монотонно возрастает, а если 0 < a < 1 - монотонно убывает. При этом для любого основания выполняется равенство a 0 = 1. Следовательно, график любой показательной функции проходит через точку (0; 1), Л о г а р и ф м и ч е с к а я функция. Эта функция является обратной по отношению к показательной. График логарифмической функции симметричен графику показательной функции относительно прямой у = х. При этом для любого основания а > 0 и а ≠ 1 выполняется условие log a 1 = 0, поэтому график всякой логарифмической функции проходит через точку (1; 0), Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x. Функции y = sin х и у = cos х определены на всей числовой прямой и имеют множеством значений промежуток [− 1, 1], Функция у = tg х определена при всех значениях
(0, + ∞). Если a > 1, то функция монотонно возрастает, а если 0 < a < 1 - монотонно убывает. При этом для любого основания выполняется равенство a 0 = 1. Следовательно, график любой показательной функции проходит через точку (0; 1), Л о г а р и ф м и ч е с к а я функция. Эта функция является обратной по отношению к показательной. График логарифмической функции симметричен графику показательной функции относительно прямой у = х. При этом для любого основания а > 0 и а ≠ 1 выполняется условие log a 1 = 0, поэтому график всякой логарифмической функции проходит через точку (1; 0), Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x. Функции y = sin х и у = cos х определены на всей числовой прямой и имеют множеством значений промежуток [− 1, 1], Функция у = tg х определена при всех значениях 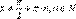 , монотонно возрастает в каждом интервале области определения. Функция у = ctg х определена при всех значениях x ≠ π n, n
, монотонно возрастает в каждом интервале области определения. Функция у = ctg х определена при всех значениях x ≠ π n, n 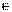 N, и монотонно убывает в каждом интервале области определения.
N, и монотонно убывает в каждом интервале области определения.
Множеством значений тангенса и котангенса служит промежуток (− ∞; + ∞).
Функции у = sin х, у = tg х и у = ctg х − нечетные, их графики симметричны относительно начала координат. Функция у = cos x - четная, ее график симметричен относительно оси Оу.
Тригонометрические функции являются периодическими. Определение. Функция f (х) называется периодической, если существует такое число Т > 0, что для любых значений аргумента из области определения функции имеет место равенство f (x ± T) = f (x). Основной период функций у = sin х и у = cos x равен 2·p, основной период функций у = tg x и y = ctg x равен p. Обрат тригоном фун-и. Функция y = arcsin x, где х 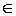 [− 1; + 1], y
[− 1; + 1], y 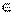 [− p/ 2, p/2 ], означает, что у есть угол из промежутка [− p/ 2, p/2 ], синус которого равен х, то есть х = sin у.
[− p/ 2, p/2 ], означает, что у есть угол из промежутка [− p/ 2, p/2 ], синус которого равен х, то есть х = sin у.
Функция y = arcsin x является обратной для функции y = sin x, x 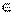 [− p/ 2, p/ 2 ], у
[− p/ 2, p/ 2 ], у 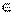 [− 1; + 1],
[− 1; + 1],
Функция у = arcсos х, x 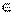 [− 1, 1], y
[− 1, 1], y 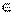 [0, p] обратная функции у = сos х, где х
[0, p] обратная функции у = сos х, где х 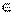 [0, p] и y
[0, p] и y 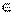 [− 1, 1]. Её график симметричен графику у = сos х относительно прямой у = х, Функция у = arctg x, где x
[− 1, 1]. Её график симметричен графику у = сos х относительно прямой у = х, Функция у = arctg x, где x 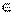 (− ∞; + ∞) и y
(− ∞; + ∞) и y 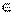 (− p/ 2, p/ 2), является обратной функции y = tg x, y
(− p/ 2, p/ 2), является обратной функции y = tg x, y 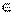 (− ∞; + ∞) и. Ее график симметричен графику функции y = tg x, x
(− ∞; + ∞) и. Ее график симметричен графику функции y = tg x, x 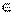 (− p/ 2, p/ 2), относительно прямой у = х, Функция у = arcctg x, x
(− p/ 2, p/ 2), относительно прямой у = х, Функция у = arcctg x, x 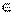 (− ∞; + ∞), y
(− ∞; + ∞), y 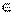 (0; p) обратная функции у = ctg x, x
(0; p) обратная функции у = ctg x, x 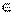 (0; p), у
(0; p), у 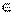 (− ∞; + ∞). Ее график симметричен графику у = ctg x, x
(− ∞; + ∞). Ее график симметричен графику у = ctg x, x 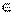 (0; p), относительно прямой у = х,
(0; p), относительно прямой у = х,
38.Предел последовательности. В математике пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера. Предел — одно из основных понятий математического анализа. Понятие предела использовалось ещё Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году. Пусть дано топологическое пространство 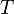 и последовательность
и последовательность 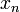 . Тогда, если существует элемент
. Тогда, если существует элемент 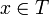 такой, что
такой, что 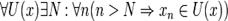 ,
,
где 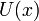 — открытое множество, содержащее
— открытое множество, содержащее 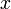 , то он называется пределом последовательности
, то он называется пределом последовательности 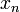 . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент
. Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент 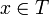 такой, что
такой, что 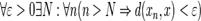 , где
, где 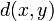 — метрика, то
— метрика, то 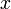 называется пределом
называется пределом 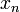 .
.
Не у всякой последовательности существует предел. Например, если взять в качестве пространства множество вещественных чисел со стандартной топологией, а в качестве 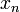 последовательность
последовательность 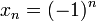 , то у неё не будет предела. Если у последовательности существует предел, то она называется сходящейся, если нет — расходящейся. В общем случае пределов может быть несколько. Например, если пространство снабжено антидискретной топологией, то пределом любой последовательности будет любой элемент пространства. Однако при наложении некоторых условий на пространство можно достичь единственности предела в случае его существования.
, то у неё не будет предела. Если у последовательности существует предел, то она называется сходящейся, если нет — расходящейся. В общем случае пределов может быть несколько. Например, если пространство снабжено антидискретной топологией, то пределом любой последовательности будет любой элемент пространства. Однако при наложении некоторых условий на пространство можно достичь единственности предела в случае его существования.
Не нашли, что искали? Воспользуйтесь поиском: