
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Моделирование в процессе решения текстовых задач. Рассматривая процесс решения текстовой задачи, мы неоднократно использовали термин «модель», «моделирование»
Рассматривая процесс решения текстовой задачи, мы неоднократно использовали термин «модель», «моделирование». Это не случай, но. Во всех науках модели выступают как мощное орудие познания. Реальные объекты и процессы бывают столь многогранны и сложны что лучшим способом их изучения часто является построение и исследование модели, отображающей лишь какую-то грань реальности и потому более простую, чем эта реальность.
Ранее мы установили, что текстовая задача - это словесная модель некоторого явления (ситуации, процесса). Чтобы решить такую задачу, надо перевести ее на язык математических действий, т. е. построить ее математическую модель.
Вообще, математическая модель - это описание какого-либо реального процесса на математическом языке.
Математической моделью текстовой задачи является выражение (либо запись по действиям), если задача решается арифметическим методом, и уравнение (либо система уравнений), если задача решается алгебраическим методом.
В процессе решения задачи четко выделяются три этапа математического моделирования:
I этап - это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и тематическими способами описываются связи между ними;
II этап - внутримодельное решение (т.е. нахождение знамени» выражения, выполнение действий, решение уравнения);
IIIэтап - интерпретация, т.е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача.
Проиллюстрируем сказанное на примере решения алгебраическим методом следующей задачи: «В одном вагоне электропоезд было пассажиров в 2 раза больше, чем в другом. Когда из первого вагона вышли 3 человека, а во второй вагон вошли 7 человек, т обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне первоначально?».
Обозначим через х первоначальное число пассажиров во втором гоне. Тогда число пассажиров в первом вагоне - 2х. Когда из первого вагона вышли 3 человека, в нем осталось 2х - 3 пассажира. Во второй вагон вошли 7 человек, значит, в нем стало х + 7 пассажиров. Так как в обоих вагонах пассажиров стало поровну, то можно зяписать что 2х - 3 = х + 7. Получили уравнение – это математическая модель данной задачи.
Следующий этап - решение полученного уравнения вне зависимости того, что в нем обозначает переменная х: переносим в левую часть члены уравнения, содержащие х, а в правую - не содержащие х, причем переносимых членов знаки меняем на противоположные: 2х - х = 7 + 3. Приводим подобные члены и получаем, что х = 10.
Последний, третий этап - используем полученное решение, чтобы ответить на вопрос задачи: во втором вагоне было первоначально 10 человек, а в первом - 20 (10×2 = 20).
Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический, т.е. I этап математического моделирования. Чтобы облегчить эту процедуру, строят вспомогательные модели - схемы, таблицы и др. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы, рисунки и т.д.); от нее - к математической, на которой и происходит решение задачи.
Такой подход к процессу решения задачи разделяют и психологи. Они считают, что процесс решения задачи есть сложный процесс поиска системы моделей и определенной последовательности перехода от одного уровня моделирования к другому, более обобщенному, что решение задачи человеком есть процесс ее переформулирования. При этом используется такая операция мышления, как анализ через синтез, когда объект в процессе мышления включается во все новые связи и в силу этого выступает во все новых качествах. Главным средством переформулирования является моделирование.
Прием моделирования заключается в том, что для исследования какого-либо объекта (в нашем случае текстовой задачи) выбирают (или строят) другой объект, в каком-то отношении подобный тому, который исследуют. Построенный новый объект изучают, с его помощью решают исследовательские задачи, а затем результат переносят первоначальный объект.
Модели бывают разные, и поскольку в литературе нет единообразия в их названиях, уточним терминологию, которую будем использовать в дальнейшем.
Все модели можно разделить на схематизированные и знаковые по видам средств, используемых для их построения.
Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они обеспечивают. Вещественные (или предметные) модели текстовых задач обеспечивают физическое действие с предметами. Они могут строиться из каких-либо предметов (пуговиц, спичек, бумажных полосок и т.д.), они могут быть представлены разного рода инсценировками сюжета задач. К этому виду моделей причисляют и мысленное воссоздание реальной ситуации, описанной в задаче, в виде представлений.
Графические модели используются, как правило, для обобщенного, схематического воссоздания ситуации задачи. К графическим следует отнести следующие виды моделей:
5)рисунок;
6)условный рисунок;
7)чертеж;
8)схематичный чертеж (или просто схема).
Разъясним суть этих моделей на примере задачи: «Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовал Вова?»
Рисунок в качестве графической модели этой задачи имеет вид (рис. 40).
 |
Условный рисунок может быть таким, как на рисунке 41.
 |
Чертеж как графическая модель выполняется при помощи чертежных инструментов с соблюдением заданных отношений (рис. 42).
 |
 |
Схематический чертеж (схема) может выполняться от руки, на нем указываются все данные и искомые (рис. 43).
Знаковые модели могут быть выполнены как на естественном, так и на математическом языке. К знаковым моделям, выполненным на естественном языке, можно отнести краткую запись задачи, таблицы. Например, краткая запись задачи о домиках Лиды и Вовы может быть такой:

|
Таблица как вид знаковой модели используется главным образом тогда, когда в задаче имеется несколько взаимосвязанных величин, каждая из которых задана одним или несколькими значениями. Пример такой таблицы см. на с. 113.
Знаковыми моделями текстовых задач, выполненными на математическом языке, являются: выражение, уравнение, система уравнений, запись решения задачи по действиям. Поскольку на этих моделях происходит решение задачи, их называют решающими моделями. Остальные модели, все схематизированные и знаковые, выполненные на естественном языке, - это вспомогательные модели, которые обеспечивают переход от текста задачи к математической модели.
Не следует думать, что всякая краткая запись или чертеж, выполненные для данной задачи, являются ее моделями. Так как модель - это
своеобразная копия задачи, то на ней должны быть представлены все ее объекты, все отношения между ними, указаны требования.
Для большинства текстовых задач приходится строить различные вспомогательные модели. С одной стороны, эти модели представляют собой результат анализа задачи, но с другой - построение таких моделей организует и направляет детальный и глубокий анализ задачи.
Рассмотрим процесс решения арифметическим методом текстовой задачи о пассажирах в двух вагонах.
Предварительный анализ задачи позволяет выделить ее объекты -это пассажиры в двух вагонах поезда. О них известно, что:
5)В первом вагоне в 2 раза больше пассажиров, чем во втором.
6)Из первого вагона вышли 3 пассажира.
7)Во второй вошли 7 пассажиров.
8)В первом и втором вагонах пассажиров стало поровну. В задаче два требования:
9)1) Сколько пассажиров было первоначально в первом вагоне?
2) Сколько пассажиров было первоначально во втором вагоне? Построим графическую модель данной задачи в виде схематического чертежа (рис. 44).
 По схеме сразу видно, что математическая модель данной задачи имеет вид:
По схеме сразу видно, что математическая модель данной задачи имеет вид:
7 + 3 - это число пассажиров во II вагоне, а (7 + 3)2 - это число пассажиров в I вагоне. Произведя вычисления, получаем ответ на вопрос задачи: во II вагоне было 10 пассажиров, а в I -20 пассажиров.
Упражнения
1. Используя материал данного параграфа, заполните следующую таблицу при условии, что решение задачи (РЗ) выполняется арифметическим методом.
| Название этапа РЗ | Цель этапа | Приемы выполнения этапа |
| Анализ задачи | ||
| Поиск плана решения | ||
| Осуществление плана решения | ||
| Проверка |
2. Выполните анализ нижеприведенных задач, используя различные приемы:
а) Ученик купил тетрадей в клетку в 3 раза больше, чем тетрадей в линейку, причем их было на 18 больше, чем тетрадей в линейку. Сколько всего тетрадей купил ученик?
б) В трех классах всего 83 учащихся. В первом классе на 4 ученика больше, чем во втором, и на 3 меньше, чем в третьем. Сколько учеников в каждом классе?
в) Мальчики полили 8 яблонь и 4 сливы, принеся 140 ведер воды. Сколько ведер воды вылили под яблони, а сколько под сливы, если на полив одной яблони уходит воды в 3 раза больше, чем на полив одной сливы?
8. Выполните поиск плана решения арифметическим методом задачи а) из упражнения 2 по модели, а поиск плана решения задачи в) по тексту.
9. Запишите решение задачи из упражнения 2 по действиям с пояснением.
10. Какие из задач упражнения 2 вы можете решить различными арифметическими способами?
11. Каким образом можно проверить правильность найденного результата для задачи а) из упражнения 2?
12. Решите арифметическим методом задачи, выделяя этапы решения и приемы их выполнения:
а) Ручка в два раза дороже карандаша, а резинка в три раза дешевле карандаша. Ручка, карандаш и резинка стоят вместе 4000 р. Сколько стоит резинка?
б) Сын на 24 года младше мамы, а папа на 3 года старше мамы. Сколько лет папе, если сыну 10 лет?
в) Один кусок проволоки на 54 м длиннее другого. После того как от каждого из кусков отрезали по 12 м, второй кусок оказался в 4 раза короче первого. Найдите первоначальную длину каждого куска проволоки.
8. Дана задача: «Два велосипедиста одновременно выехали навстречу друг другу из двух поселков, расстояние между которыми 76 км. Через 2 ч они встретились. Какова скорость каждого велосипедиста, если известно, что скорость одного из них на 3 км/ч меньше другого?»
Сравните разные способы ее решения.
1 способ 2 способ
1)76:2 = 38 (км/ч) 1)3×2 = 6 (км)
2)38 - 3 = 35 (км/ч) 2) 76 - 6 = 70 (км)
3)35:2 = 17,5(км/ч) 3)70:2 = 35 (км)
4)17,5+3=20,5(км/ч) 4)35:2= 17,5 (км/ч)
5) 17,5 + 3 = 20,5(км/ч)
При каком способе рассуждения проще?32. Решение задач «на части»
Само название вида задач говорит о том, что рассматриваемые в них величины состоят из частей. В некоторых из них части представлены явно, в других эти части надо суметь выделить, приняв подходящую величину за 1 часть и определив, из скольких таких частей состоят другие величины, о которых идет речь в задаче.
При решении таких задач арифметическим методом чаще всего используют вспомогательные модели, выполненные с помощью отрезков или прямоугольников.
Задача 1. Для варки варенья из вишни на 2. части ягод берут 3 части сахара. Сколько сахара надо взять на 10 кг ягод?
Решение. В задаче речь идет о массе ягод и массе сахара, необходимых для варки варенья. Известно, что всего ягод 10 кг и что на 2 части ягод надо брать 3 части сахара. Требуется найти массу сахара, чтобы сварить варенье из 10 кг ягод.
Изобразим при помощи отрезка данную массу ягод (рис. 45). Тогда половина этого отрезка представляет собой массу ягод, которая при
 |
ходится на 1 часть. Сахара, по условию задачи, надо 3 таких части. Запишем решение по действиям с пояснением:
1) 10:2 = 5 (кг) - столько килограммов ягод приходится на каждую часть;
 |
2) 5 ×3 = 15 (кг) - столько надо взять сахара.
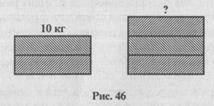
Вспомогательную модель к данной задаче можно было выполнить
при помощи прямоугольников (рис. 46).
Задача 2. В первой пачке было на 10 тетрадей больше, чем во второй. Всего было 70 тетрадей. Сколько тетрадей было в каждой пачке?
Решение. В задаче рассматриваются две пачки тетрадей. Всего тетрадей 70. В одной пачке тетрадей на 10 больше, чем во второй. Требуется узнать, сколько тетрадей было в каждой пачке.
 |
Изобразим при помощи отрезка количество тетрадей во второй пачке. Тогда тетради в первой пачке можно представить в виде отрезка который больше второго (рис. 47). По чертежу видно, что если тетради
во второй пачке составляют 1 часть всех тетрадей, то тетради в первой составляют также 1 часть и еще 10 тетрадей.
Если эти 10 тетрадей убрать из первой пачки, то в пачках тетрадей станет поровну - столько, сколько во второй пачке.
Запишем решение задачи по действиям с пояснением.
4)70-10 = 60 (тетр.) - столько тетрадей приходится на 2 равные части, или столько было бы тетрадей в двух пачках, если бы их было поровну - столько, сколько во второй пачке.
5)60:2 = 30 (тетр.) - столько тетрадей приходится на 1 часть, или столько тетрадей было во второй пачке.
3)30 +10 = 40 (тетр.) - столько тетрадей было в первой пачке. Вспомогательная модель подсказывает и второй способ решения данной задачи. Если за 1 часть принять тетради в первой пачке, то чтобы во второй стало столько же, надо к ней добавить 10 тетрадей. И тогда решение будет таким:
1)70+10 = 80 (тетр.)
2)80:2 = 40 (тетр.)
3)40-10 = 30 (тетр.)
Существует и третий арифметический способ решения данной задачи. Разделим 10 тетрадей пополам и одну половину оставим к первой пачке, а другую добавим во вторую. Тогда тетрадей в пачках станет поровну и можно, разделив 70 на 2 равные части, узнать, сколько тетрадей в каждой такой пачке, а затем их первоначальное количество в каждой пачке.
1)10:2 = 5 (тетр.) - столько тетрадей надо переложить из первой
пачки во вторую, чтобы в них тетрадей стало поровну.
2)70:2 = 35 (тетр.) - столько тетрадей в каждой пачке, если из первой переложить во вторую 5 тетрадей.
5)35 + 5 = 40 (тетр.) - столько тетрадей в первой пачке.
6)35-5 = 30 (тетр.) - столько тетрадей во второй пачке.
Задача 3. Сумма двух чисел 96, а разность 18. Найдите эти числа. Решение. В этой задаче требуется найти два числа по их сумме и разности. Так как разность искомых чисел равна 18, то одно число больше другого на 18. Получаем задачу, аналогичную задаче 2: «Одно число больше другого на 18. Сумма чисел равна 96. Найти эти числа». Решить ее можно тремя арифметическими способами.
Задача 4. В двух кусках ткани одинаковое количество материи. После того как от одного куска отрезали 18 м, а от другого 25 м, в первом куске осталось вдвое больше ткани, чем во втором. Сколько метров ткани было в каждом куске первоначально?
Решение. Объекты задачи - два куска ткани одинаковой длины. От первого отрезали 18 м, от второго - 25 м. После этого в первом осталось вдвое больше ткани, чем во втором. Требование задачи -найти первоначальное количество метров ткани в каждом куске.
 Изобразим куски ткани при помощи отрезков одинаковой длины, а затем покажем на них то количество ткани, которое отрезали и которое осталось. Если количество ткани, которое осталось во втором куске, - это 1 часть, то количество оставшейся ткани в первом куске - это 2 таких части. По чертежу (рис. 48) видно, что на 1 часть приходится количество ткани, которое легко найти. Запишем найденное решение по действиям:
Изобразим куски ткани при помощи отрезков одинаковой длины, а затем покажем на них то количество ткани, которое отрезали и которое осталось. Если количество ткани, которое осталось во втором куске, - это 1 часть, то количество оставшейся ткани в первом куске - это 2 таких части. По чертежу (рис. 48) видно, что на 1 часть приходится количество ткани, которое легко найти. Запишем найденное решение по действиям:
3)25-18 = 7 (м) - на столько больше ткани отрезали от второго куска, или количество ткани, которое осталось во втором куске
4)7 + 25 = 32 (м) - столько ткани было первоначально во втором куске (и, следовательно, в первом) куске.
Упражнения
1. Изобразите при помощи отрезков ситуации:
а) купили р кг яблок, а груш на t кг больше;
б) купили p кг яблок, а груш в 2 раза больше.
Какими могут быть требования к данным ситуациям? Для каждого случая постройте модель и обозначьте на ней требования.
2. Требуется смешать 3 части песка и 2 части цемента. Сколько цемента и песка в отдельности надо взять, чтобы получить 30 кг смеси?
 3. Установите соответствие между вспомогательными моделями (рис. 49) и следующими задачами; используя модели, решите задачи:
3. Установите соответствие между вспомогательными моделями (рис. 49) и следующими задачами; используя модели, решите задачи:
а) В двух пакетах было15 яблок. Когда из одного пакета взяли 3 яблока, в нем осталось в 2 раза меньше яблок, чем в другом. Сколько яблок было в каждом пакете?
б) В трех пакетах лежит 20 яблок, причем в одном пакете их в 2 раза меньше, чем в каждом из двух других. Сколько яблок в каждом пакете?
в) У двух мальчиков было 8 яблок. Когда один съел одно яблоко, а другой – 3 яблока, у них осталось яблок поровну. Сколько яблок было у каждого?
4. Решите следующие задачи, построив на этапе анализа вспомогательные модели; решение запишите по действиям с пояснением:
а) Мама дала трем девочкам 12 конфет и предложила разделить их так, чтобы младшая получила в 3 раза, а средняя в 2 раза больше старшей. Сколько конфет достанется каждой?
б) На двух тарелках лежало 9 яблок. Когда с одной тарелки взяли одно яблоко, то на этой тарелке осталось яблок в 3 раза больше, чем на другой. Сколько яблок было на каждой тарелке?
в) У моего брата было в 6 раз больше орехов, чем у меня. После того как он отдал 10 орехов сестре, у нас орехов стало поровну. Сколько орехов было у меня и у брата первоначально?
г) Полсотни яблок разложили в корзину и два пакета. В корзину положили на 14 яблок больше, чем в каждый пакет. Сколько яблок в корзине и в пакете?
д) Школьник прочитал 18 страниц за три дня. Если бы он в первый день прочитал на одну страницу больше, а во второй день на 4 страницы меньше, то каждый день он читал бы поровну. По сколько страниц читал школьник каждый день?
5. Постройте вспомогательные модели и с их помощью найдите решения следующих задач:
а) На одной полке на 6 книг больше, чем на другой. Сколько книг нужно переложить с одной полки на другую, чтобы книг стало поровну?
б) Если с одной полки переложить на другую 6 книг, то на обеих полках книг будет поровну. На сколько книг на одной полке больше, чем на другой?
в) На одной полке на 6 книг больше, чем на другой. На сколько книг будет больше на одной полке, чем на другой, если с первой полки переложили на другую 10 книг?
г) На первой полке на 6 книг больше, чем на второй. На сколько книг будет на первой полке больше, если со второй полки переложить на первую 10 книг?
6. Поиск плана решения проведите по вспомогательной модели; решение запишите по действиям; выполните проверку найденного решения:
а) В двух бидонах 28 л краски. Если из одного взять 3 л, а в другой добавить 2 л, то в первом станет на 7 л краски больше, чем во втором. Сколько краски в каждом бидоне?
б) На складе в три раза больше муки, чем в магазине. Если со склада взять 850 т муки, а магазином будет продано 50 т муки, то и на складе, и в магазине муки останется поровну. Сколько муки на складе и сколько в магазине?
в) У Наташи на 15 открыток больше, чем у Сережи. Детям подарили еще по 6 открыток. У Наташи стало в 2 раза больше открыток, чему Сережи. Сколько открыток было у каждого первоначально?
7. Решите различными арифметическими способами:
а) В двух книжных шкафах было 1536 книг. Когда из одного взяли 156 книг, а из другого в три раза больше, то книг в шкафу стало поровну. Сколько книг было в каждом шкафу первоначально?
б) Площадь земли, засеянная пшеницей, в 6 раз больше площади засеянной ячменем, а площадь, засеянная рожью, в 3 раза меньше площади, засеянной пшеницей. Сколько гектаров земли засеяно каждой культурой, если пшеницей засеяно на 480 га больше, чем рожью?
Не нашли, что искали? Воспользуйтесь поиском: