Числовые равенства и неравенства

Пусть ¦ и g - два числовых выражения. Соединим их знаком равенства. Получим предложение ¦= g, которое называют числовым равенством.

Возьмем, например, числовые выражения 3 + 2 и 6 - 1 и соединим их знаком равенства 3 + 2 = 6-1. Оно истинное. Если же соединить знаком равенства 3 + 2 и 7 - 3, то получим ложное числовое равенство 3 + 2 = = 7-3. Таким образом, с логической точки зрения числовое равенство -это высказывание, истинное или ложное.

Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.

Напомним некоторые свойства истинных числовых равенств.

1. Если к обеим частям истинного числового равенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.

2. Если обе части истинного числового равенства умножить на одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.

Пусть ¦ и g - два числовых выражения. Соединим их знаком «>» (или «<»). Получим предложение ¦ > g (или ¦< g), которое называют числовым неравенством.

Например, если соединить выражение 6 + 2 и 13-7 знаком «>», то получим истинное числовое неравенство 6 + 2 > 13-7. Если соединить те же выражения знаком «<», получим ложное числовое неравенство 6 + 2 < 13-7. Таким образом, с логической точки зрения числовое неравенство - это высказывание, истинное или ложное.

Числовые неравенства обладают рядом свойств. Рассмотрим некоторые.

1. Если к обеим частям истинного числового неравенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое неравенство.

2. Если обе части истинного числового неравенства умножить на одно и то же числовое выражение, имеющее смысл и положительное значение, то получим также истинное числовое неравенство.

3. Если обе части истинного числового неравенства умножить на одно и то же числовое выражение, имеющее смысл и отрицательное значение, а также поменяем знак неравенства на противоположный, то получим также истинное числовое неравенство.

Упражнения

1. Установите, какие из следующих числовых равенств и неравенств истинны:

а) ;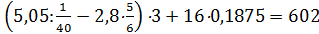

б)

в) 1,0905:0,025-6,84×3,07 + 2,38:100 < 4,8: (0,04-0,006).

2. Проверьте, истинны ли числовые равенства:

13 × 93 = 31× 39, 14×82 =41×28, 23×64 = 32×46. Можно ли утверждать, что произведение любых двух натуральных чисел не изменится, если в каждом множителе переставить цифры?

3. Известно, что х > у - истинное неравенство. Будут ли истинными следующие неравенства:

а) -3,7 а * -3,7b; г) - ;

б) 0,12a * 0,12 b д) -2(a+ 5 ) *-2(b+ 5);

в) ; е) (a -1)*

4. Известно, что а < b - истинное неравенство. Поставьте вместо * знак «>» или «<» так, чтобы получилось истинное неравенство:

a) -3,7 a *-3,7 b; г) ;

б) 0,12*0,12 b д) -2(a+ 5) * -2(b+5);

в) ; е) .

5. Дано неравенство 5 > 3. Умножьте обе его части на 7; 0,1; 2,6; .

Можно ли на основании полученных результатов утверждать, что для любого положительного числа а неравенство 5 а > 3 а истинно?

6. Выполните задания, которые предназначаются ученикам начальных классов, и сделайте вывод о том, как трактуются в начальном курсе математики понятия числового равенства и числового неравенства:

а) Запиши два верных равенства и два верных неравенства, используя выражения: 9 × 3, 30 - 6, 3 × 9, 30 - 3.

б) Расставь скобки так, чтобы равенства были верными: 4+2×3=18;

31-10-3 = 24; 54-12 + 8 = 34.

в) Поставь вместо * знаки действий так, чтобы получились верные равенства: 3*6*2 = 9; 9*3*6=18.

7. Какие ответы учеников вы будете считать правильными при выполнении ими задания - сравнить выражения, не вычисляя их значения:

а) 70-32+ 9×32...79×30+ 79×2;

б) 7×4 + 3×4... (7 +8)×4;

в) 8500:1700...8500:100:17;

г) 24×6080...(6000+ 80)×24?

Не нашли, что искали? Воспользуйтесь поиском: