
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производные обратных тригонометрических функций
Теорема 13. Если  то
то  или коротко:
или коротко: 
Теорема 14. Если  , то
, то 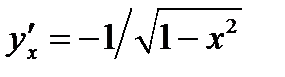 или коротко:
или коротко: 
Теорема 15. Если  то
то  или коротко:
или коротко: 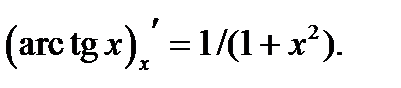
Теорема 16. Если  то
то  или коротко:
или коротко: 
26) Теорема Ролля. Если функция  непрерывна в замкнутом интервале
непрерывна в замкнутом интервале  , дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом интервале найдётся хотя бы одна точка
, дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом интервале найдётся хотя бы одна точка 
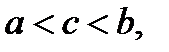 в которой значение производной
в которой значение производной 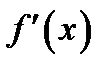 обращается в нуль.
обращается в нуль.
Теорема Ферма. Если дифференцируемая в интервале  функ-ция
функ-ция  принимает в точке
принимает в точке  (
( ) своё наибольшее значение в
) своё наибольшее значение в  то в этой точке производная
то в этой точке производная  обращается в нуль, т. е.
обращается в нуль, т. е. 
Теорема Коши. Если функции  и
и  непрерывны в замкнутом интервале
непрерывны в замкнутом интервале  и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале
и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале 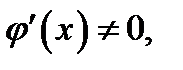 то в
то в  найдется хотя бы одна точка
найдется хотя бы одна точка  (
( ), для которой справедлива формула
), для которой справедлива формула

Теорема Лагранжа. Если функция  непрерывна в замкнутом интервале
непрерывна в замкнутом интервале  и дифференцируема во всех внутренних точках этого интервала, то в
и дифференцируема во всех внутренних точках этого интервала, то в  найдется хотя бы одна точка
найдется хотя бы одна точка  (
( ), для которой справедлива формула
), для которой справедлива формула
27). Правило Лопиталя
Теорема. Пусть функции  и
и  одновременно стремятся к нулю или к бесконечности при
одновременно стремятся к нулю или к бесконечности при 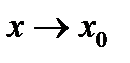 (
( – заданное число) или при
– заданное число) или при  Если при этом отношение производных
Если при этом отношение производных  имеет предел, то отношение функций также имеет предел, равный пределу отношения производных, т. е.
имеет предел, то отношение функций также имеет предел, равный пределу отношения производных, т. е.
28) Возрастание и убывание функции. Монотонность. Интервалы монотонности. Достаточный признак монотонности функции.
Функция называется возрастающей в интервале, если большему значению аргумента отвечает большее значение функции, а интервал называется интервалом возрастания функции.
Функция называется убывающей в интервале, если большему значению аргумента отвечает меньшее значение функции, а интервал называется интервалом убывания функции.
Интервалы возрастания и убывания функции называются интервалами монотонности, а сама функция называется монотонной.
29) Точки экстремума функции. Экстремумы функции.
Пусть  – внутренняя точка области определения функции
– внутренняя точка области определения функции  Точка
Точка  называется точкой максимума функции
называется точкой максимума функции  если для всех отличных от
если для всех отличных от  точек некоторой окрестности точки
точек некоторой окрестности точки  (другими словами, некоторого малого интервала, содержащего внутри себя точку
(другими словами, некоторого малого интервала, содержащего внутри себя точку  ), выполняется неравенство
), выполняется неравенство  .
.
Точка  называется точкой минимума функции
называется точкой минимума функции  если для всех отличных от
если для всех отличных от  точек некоторой окрестности точки
точек некоторой окрестности точки  выполняется неравенство
выполняется неравенство  .
.
Точки максимума и минимума функции называются точками экстремума этой функции, а значения функции в этих точках – экстремальными (максимальными или минимальными) значениями.
30) Наибольшие и наименьшие значения функции в интервале. Необходимый признак экстремума. Критические точки.
Теорема 3 (необходимый признак экстремума функции) .Если дифференцируемая функция  в точке
в точке  имеет экстремум, то её производная
имеет экстремум, то её производная  в этой точке обращается в нуль, т. е.
в этой точке обращается в нуль, т. е. 
Точки, в которых производная  функции
функции  обращается в нуль или не существует, называются критическими точками функции
обращается в нуль или не существует, называются критическими точками функции  Как мы видели, не всякая критическая точка является точкой экстремума функции
Как мы видели, не всякая критическая точка является точкой экстремума функции 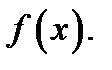
30) Наибольшие и наименьшие значения функции в интервале. Необходимый признак экстремума. Критические точки.
Теорема 3 (необходимый признак экстремума функции) .Если дифференцируемая функция  в точке
в точке  имеет экстремум, то её производная
имеет экстремум, то её производная  в этой точке обращается в нуль, т. е.
в этой точке обращается в нуль, т. е. 
Точки, в которых производная  функции
функции  обращается в нуль или не существует, называются критическими точками функции
обращается в нуль или не существует, называются критическими точками функции  Как мы видели, не всякая критическая точка является точкой экстремума функции
Как мы видели, не всякая критическая точка является точкой экстремума функции 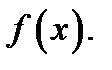
32) Схема исследования функции на экстремум.
Рассмотрим схему исследования функции на экстремум. Чтобы найти экстремум функции 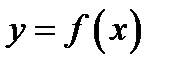 , нужно:
, нужно:
· найти критические точки этой функции, т. е. точки, в которых производная  обращается в нуль или не существует;
обращается в нуль или не существует;
· каждую критическую точку исследовать с помощью достаточного признака экстремума;
найти экстремальные значения функции, подставив вместо 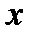 в выражение
в выражение 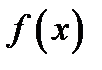 точки экстремума
точки экстремума
33) Выпуклость и вогнутость кривой. Точки ее перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой.
Кривая  называется выпуклой в интервале
называется выпуклой в интервале  если она лежит ниже любой своей касательной в точках, абсциссы которых лежат в этом интервале (см. рис. 68).
если она лежит ниже любой своей касательной в точках, абсциссы которых лежат в этом интервале (см. рис. 68).
Кривая  называется вогнутой в интервале
называется вогнутой в интервале  если она лежит выше любой своей касательной в точках, абсциссы которых лежат в этом интервале(см. рис. 69).
если она лежит выше любой своей касательной в точках, абсциссы которых лежат в этом интервале(см. рис. 69).
Точка кривой, отделяющая выпуклую часть от вогнутой, называется точкой перегиба.
Теорема 7 (достаточные признаки выпуклости и вогнутости кривой). Если  всюду в интервале
всюду в интервале  то в этом интервале кривая
то в этом интервале кривая 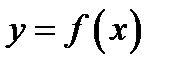 выпуклая. Если
выпуклая. Если  всюду в интервале
всюду в интервале  то в этом интервале кривая
то в этом интервале кривая 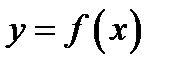 вогнутая.
вогнутая.
Теорема 9 (достаточный признак точки перегиба). Точка  кривой
кривой  является точкой перегиба, если
является точкой перегиба, если  обращается в нуль или не существует при
обращается в нуль или не существует при  и знак второй производной
и знак второй производной  изменяется при переходе
изменяется при переходе 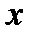 через
через  (с увеличением
(с увеличением 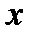 ). При перемене знака с «‑» на «+» участок выпуклости сменяется участком вогнутости, а при перемене с «+» на «‑» участок вогнутости сменяется участком выпуклости.
). При перемене знака с «‑» на «+» участок выпуклости сменяется участком вогнутости, а при перемене с «+» на «‑» участок вогнутости сменяется участком выпуклости.
34) Асимптоты кривой
Прямая называется асимптотой кривой, если расстояние от точки этой кривой до прямой стремится к нулю, когда указанная точка неограниченно удаляется от начала координат..
35) Общая схема исследования функции одной переменной и построения их графиков. Примеры.
Общая схема исследования функции  заключается в следующем:
заключается в следующем:
· находим область определения функции и ее точки разрыва;
· отыскиваем сначала критические точки, в которых производная 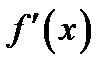 обращается в нуль или не существует; затем находим интервалы возрастания и убывания функции, в которых
обращается в нуль или не существует; затем находим интервалы возрастания и убывания функции, в которых 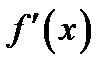 сохраняет знак, точки максимума и минимума, максимальное и минимальное ее значения;
сохраняет знак, точки максимума и минимума, максимальное и минимальное ее значения;
· определяем точки, в которых вторая производная 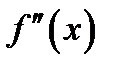 обращается в нуль или не существует, затем находим интервалы выпуклости и вогнутости функции
обращается в нуль или не существует, затем находим интервалы выпуклости и вогнутости функции  в которых
в которых 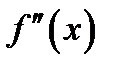 сохраняет знак, и точки перегиба;
сохраняет знак, и точки перегиба;
· отыскиваем асимптоты кривой.
34) Асимптоты кривой
Прямая называется асимптотой кривой, если расстояние от точки этой кривой до прямой стремится к нулю, когда указанная точка неограниченно удаляется от начала координат..
35) Общая схема исследования функции одной переменной и построения их графиков. Примеры.
Общая схема исследования функции  заключается в следующем:
заключается в следующем:
· находим область определения функции и ее точки разрыва;
· отыскиваем сначала критические точки, в которых производная 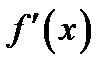 обращается в нуль или не существует; затем находим интервалы возрастания и убывания функции, в которых
обращается в нуль или не существует; затем находим интервалы возрастания и убывания функции, в которых 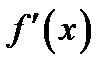 сохраняет знак, точки максимума и минимума, максимальное и минимальное ее значения;
сохраняет знак, точки максимума и минимума, максимальное и минимальное ее значения;
· определяем точки, в которых вторая производная 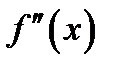 обращается в нуль или не существует, затем находим интервалы выпуклости и вогнутости функции
обращается в нуль или не существует, затем находим интервалы выпуклости и вогнутости функции  в которых
в которых 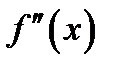 сохраняет знак, и точки перегиба;
сохраняет знак, и точки перегиба;
· отыскиваем асимптоты кривой.
Не нашли, что искали? Воспользуйтесь поиском: