
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятия о матрицах.
Определение.
Матрицей размера  называется прямоугольная таблица из чисел
называется прямоугольная таблица из чисел  , где
, где 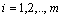 ,
,  ,
,
 ,
,
состоящая из  строк и
строк и  столбцов.
столбцов.
Основные понятия матрицы:
Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n — ее порядком.
Впрочем, для краткого обозначения матрицы часто используется одна большая буква латинского алфавита, (например, А), либо символ ||aij||, а иногда и с разъяснением: A=||aij||=(aij) (i=1,2,…,m; j=1,2,…n)
Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.
Например, матрица  это матрица порядка 2×3, ее элементы a11=1, a12=x, a13=3, a21=-2y, …
это матрица порядка 2×3, ее элементы a11=1, a12=x, a13=3, a21=-2y, …
Виды матриц
Введем понятие матриц: квадратных, диагональных, единичных и нулевых.
Определение матрицы квадратной: Квадратной матрицей n-го порядка называется матрица размера n×n.
В случае квадратной матрицы вводятся понятие главной и побочной  диагоналей.
диагоналей.
 Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний ее угол.
Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний ее угол.

Побочной диагональю той же матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.
Понятие диагональной матрицы:
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю. 
Понятие единичной матрицы: Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали. 
Понятие нулевой матрицы: Нулевой называется матрица, все элементы которой равны нулю. 
Две матрицы А и В называются равными (А=В), если они одинакового размера (т.е. имеют одинаковое количество строе и одинаковое количество столбцов и их соответствующие элементы равны). Так, если  то А=B, если a11=b11, a12=b12, a21=b21, a22=b22
то А=B, если a11=b11, a12=b12, a21=b21, a22=b22
Сложение матриц
Суммой матриц  и
и 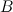 одного размера называется матрица
одного размера называется матрица  такого же размера, получаемая из исходных путем сложения соответствующих элементов:
такого же размера, получаемая из исходных путем сложения соответствующих элементов:

Замечание. Складывать можно только матрицы одинакового размера.
Пример. Задание. Найти  , если
, если 
Решение.

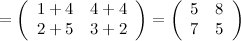
Ответ. 
Свойства сложения матриц:
1. Ассоциативность 
2.  , где
, где  - нулевая матрица соответствующего размера.
- нулевая матрица соответствующего размера.
3. Коммутативность 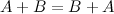
Не нашли, что искали? Воспользуйтесь поиском: