
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и  –базис
–базис  . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то  . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как  , то найдется (существует) такое число
, то найдется (существует) такое число  , что
, что  и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора  по базису
по базису  векторного пространства
векторного пространства  .
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису  векторного пространства
векторного пространства  :
:
 и
и 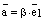 , где
, где  . Тогда
. Тогда 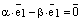 и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем:
 .
.
Так как  , то из последнего равенства следует, что
, то из последнего равенства следует, что  , ч.т.д.
, ч.т.д.
Не нашли, что искали? Воспользуйтесь поиском: