
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Действия над векторами в координатах
С векторами, заданными в прямоугольной системе координат совершать действия еще проще, чем с их геометрическими образами. В этой статье мы покажем как выполняются операции сложения векторов и умножения вектора на число, если известны их координаты, и подробно разберем решения примеров.
Пусть на плоскости задана прямоугольная декартова система координат Oxy. Рассмотрим векторы  и
и  . Эти векторы можно разложить по координатным векторам
. Эти векторы можно разложить по координатным векторам  и
и 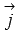 как
как  и
и  , что было показано в статье координаты вектора в прямоугольной системе координат.
, что было показано в статье координаты вектора в прямоугольной системе координат.
Найдем сумму векторов 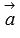 и
и  , а также произведение вектора
, а также произведение вектора 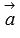 на произвольное действительное число
на произвольное действительное число  .
.
В силу свойств операций над векторами, справедливы следующие равенства
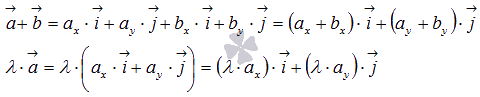
Правые части этих равенств представляют собой разложение векторов  и
и 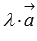 по координатным векторам
по координатным векторам  и
и 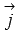 , следовательно, векторы
, следовательно, векторы  и
и 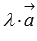 имеют координаты
имеют координаты 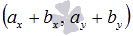 и
и 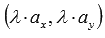 соответственно.
соответственно.
Аналогично для векторов 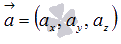 и
и  , заданных в прямоугольной системе координат Oxyz в трехмерном пространстве, мы можем записать
, заданных в прямоугольной системе координат Oxyz в трехмерном пространстве, мы можем записать

следовательно, 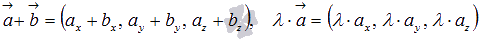 .
.
Таким образом, координаты суммы векторов 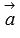 и
и  равны сумме соответствующих координат векторов
равны сумме соответствующих координат векторов 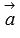 и
и  ,
,
а координаты произведения вектора 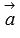 на число
на число  равны соответствующим координатам вектора
равны соответствующим координатам вектора 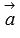 , умноженным на это число в заданной системе координат.
, умноженным на это число в заданной системе координат.
Если требуется найти координаты суммы нескольких векторов, то они будут равны сумме соответствующих координат каждого из векторов.
Разберем решения нескольких примеров.
Пример.
Выполните операцию сложения векторов  и
и  , а также найдите координаты произведения вектора
, а также найдите координаты произведения вектора 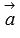 на число
на число  .
.
Решение.
Так как координаты суммы векторов равны сумме соответствующих координат каждого из векторов, то  .
.
При выполнении операции умножения вектора на число, умножаем на это число каждую координату: 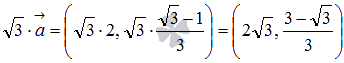 .
.
Ответ: 
Вопрос №10
Не нашли, что искали? Воспользуйтесь поиском: