Теорема Кронекера — Капелли

Правило треугольника

Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус", т.е.

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":

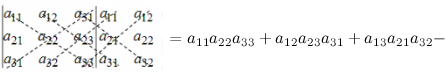
3

1. Определитель транспонированной матрицы равен определителю исходной матрицы:

2. Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножееию определителя на это число:

3. Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

4. Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю:

5. Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю:

6. Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю:

7. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

8. Если все элементы k -ой строки (столбца) определителя представлены в виде сумм a_{k j} + b_{k j}, то определитель можно представить в виде суммы соответствующих определителей:

9. Если все элементы k -ой строки (столбца) определителя представлены в виде сумм a_{k j} + b_{k j}, то определитель можно представить в виде суммы соответствующих определителей:

10. Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей:

4

Метод Крамера — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем основной матрицы

: ; ;

;

5 Ме́тод Га́усса — классический метод решения (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних находятся все переменные системы

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 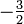и , соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

6 Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

7

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

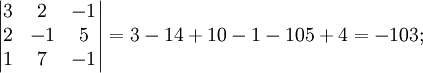
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

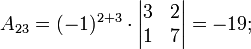
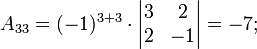
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

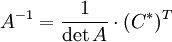
Подставляя переменные в формулу, получаем:

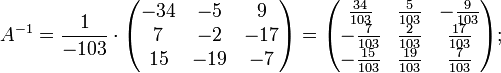
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

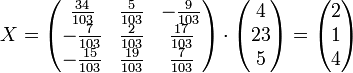Итак, x=2; y=1; z=4.

8 Рангом системы матрицы с строк и столбцов называется максимальное число линейно независимых строк.

Теорема Кронекера — Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

9 Однородной СЛАУ называется система, все правые части которой равны нулю одновременно. Однородная СЛАУ, записанная в матричном виде, всегда совместна, так как всегда является ее решением.

10 вектор -- это отрезок, у которого выделен один конец, называемый концом вектора. Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости. Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается . Вектор a называется единичным, если .

Не нашли, что искали? Воспользуйтесь поиском: