Операция умножения вектора на число.

11 Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними.

· Длина вектора, под которой обычно понимается его евклидова норма: 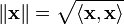(термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

· Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):
В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):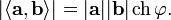

· Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочленына самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.

· Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.

· При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.

· Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

12 Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерномевклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны. Площадь треугольника бразованного векторами a и b равна половине модуля векторного произведения этих векторов

13 Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и : .

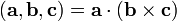Объем пирамиды (объем тетраэдра) построенной на векторах A b и c равен шестой части модуля мешаного произведения векторов составляющих пирамиду

14

15 Расстояние d между двумя точками M ₁ (x₁; у₁; z₁) и M₂(x₂; y₂; z₂) в про­странстве определяется формулой
Координаты х, у, z точки М, которая делит отрезок , ограниченный точками M₁ (х₁, y₁, z₁) и M ₂ (x₂; y₂; z₂), в отношении , определяются по формулам: , = 1 имеем координаты середины данного отрезка:l В частности, при

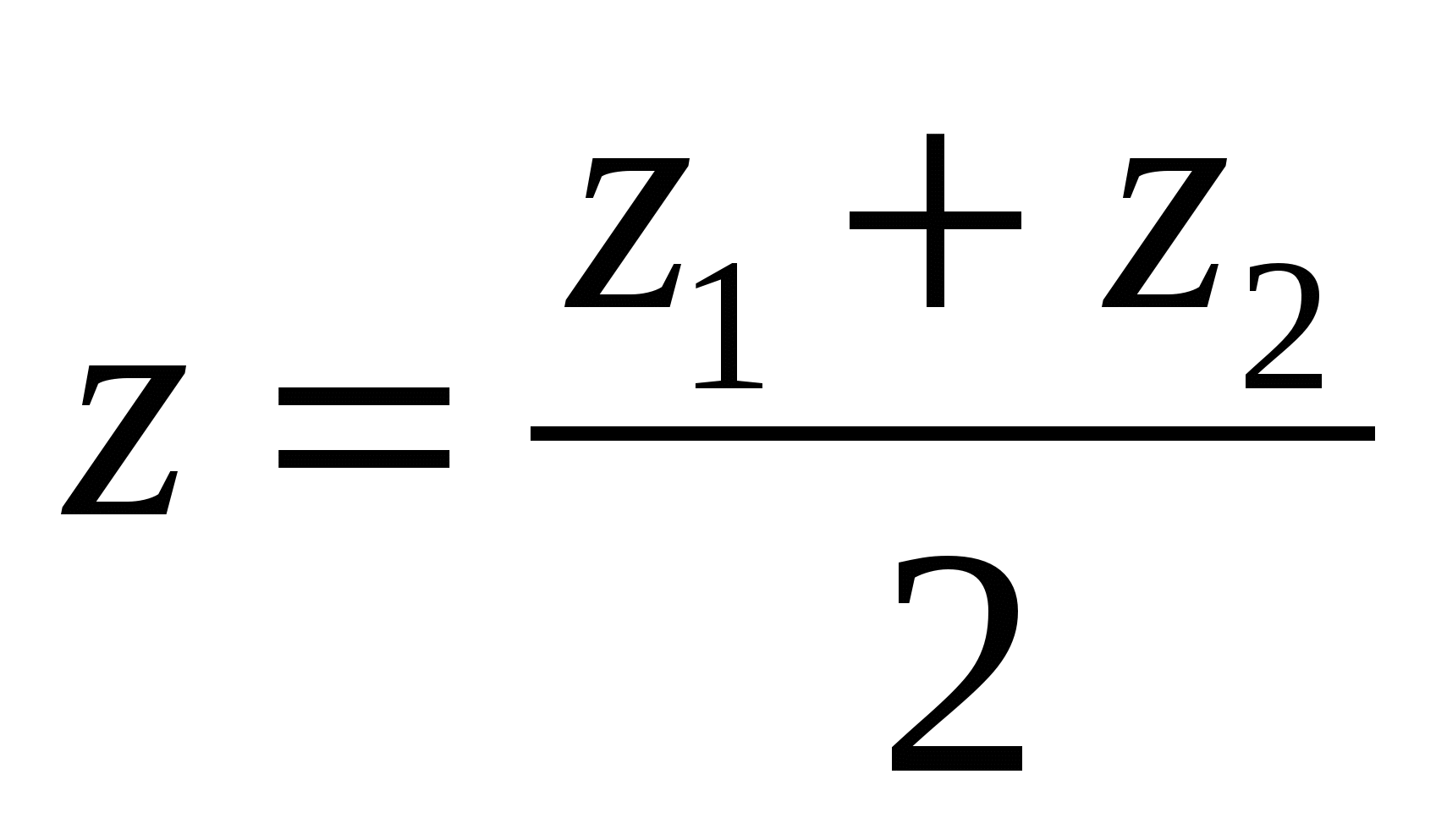
16 Во-первых, прямую можно задать, указав две точки на плоскости. Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор. Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.

17 вид уравнения прямой называется уравнением прямой с угловым коэффициентом 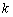. Например, если прямая задана уравнением , то её угловой коэффициент: .

Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k ₁ = k ₂.

Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

18 где и — произвольные постоянные, причем постоянные и не равны нулю одновременно. За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.

Один из этих углов равен углу между направляющими векторами этих прямых.

19 находим общее уравнение прямой a вида или уравнение прямой a с угловым коэффициентом 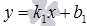; получаем общее уравнение прямой b вида 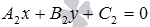или уравнение прямой b с угловым коэффициентом вида , учитывая, что прямая b проходит через заданную точку M₁ и перпендикулярна заданной прямой a; определяем координаты точки H₁ - точки пересечения прямых a и b, решая систему линейных уравнений или ; вычисляем требуемое расстояние от точки M₁ до прямой a по формуле .

20

21 Окружность — геометрическое место точек плоскости, удалённых от некоторой точки — центра окружности — на заданное расстояние, называемое радиусом окружности. или

22 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная. Каноническое уравнение эллипса

23 Каноническое уравнение гиперболы:

Прямые называются асимптотами гиперболы. Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой.

24 Каноническое уравнение параболы:

25 Общее уравнение плоскости имеет вид , где коэффициенты А,В,С, одновременно не равны нулю. Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Условие параллельности плоскостей (рис.б) заключается в параллельности нормалей , а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: .

26 нормальное уравнение плоскости .

.

Это уравнение, которому удовлетворяют координаты любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

27 Расстояние от точки до плоскости находится по формуле .

Если плоскость задана уравнением

то расстояние от точки до плоскости может быть найдено по формуле

Уравнения пучка плоскостей

28 канонические уравнения прямой ,

Угол между прямыми в пространстве равен углу между их направляющими векторами .

Две прямые параллельны тогда, когда их соответствующие коэффициенты пропорциональны:

– условие параллельности прямых.

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

– условие перпендикулярности прямых.

29 Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.

30 Преде́л фу́нкции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. 1. Предел суммы есть сумма пределов. 2. Предел произведения есть произведение пределов. 3. Предел частного есть частное пределов 4 Если u (x) Ј z (x) Ј v (x), и lim _{x ® a} u (x)=lim _{x ® a} v (x)= b, то lim _{x ® a} z (x)= b.

31 Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечностиопределённого знака. .

32 Первый замечательный предел:

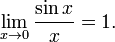
33 Второй замечательный предел:

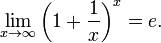
34 Сравнение бесконечно малых функций. Для того, чтобы сравнить две бесконечо малых функции, нужно вычислить предел их отношения. Если то бесконечно малые функции a(x) и b(x) называются эквивалентными, обозначают a(x)~b(x)

35 Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргументаприводят к малым изменениям значения функции. Если в точке нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода, все остальные точки существенного разрыва называем точками разрыва второго рода

36 Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b. Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C. Теорема2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m =f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b]

37 Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции

38 Предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоитгеометрический смысл производной. При 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t ₀) материальной точки в момент времени t ₀. Но по определению производной мы имеем: отсюда, v (t ₀) = x’ (t ₀), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.

39 Строго говоря, если функция имеет в определенной точке производную, то существует касательная к графику этой функции в этой точке, причем угловой коэффициент этой касательной равен значению производной.

40 Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Логарифмическая произво́дная — производная от натурального логарифма функции.

Часто применяется для упрощения нахождения производной некоторых функции, например сложно-показательных.

41 Пусть - функция от аргумента x в некотором интервале . Если в уравнении y считать аргументом, а x - функцией, то возникает новая функция , где - функция обратная данной.

42 Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Для достаточно малых окрестностей данной точки функцию можно заменить линейной. Линейная часть приращения функции называется ее дифференциалом.

11.2. Свойства дифференцируемых функций

Свойства дифференцируемых функций Будет ли функция иметь предел в точке, в которой существует ее производная? Будет ли непрерывной дифференцируемая функция? Эти вопросы возникают сразу же, потому что и понятие производной, и понятие непрерывности имеют общую первооснову – понятие предела. ТЕОРЕМА 1. Если функция имеет производную на множестве X, то она непрерывна на этом множестве. ДОКАЗАТЕЛЬСТВО. Из условия теоремы следует, что отношение имеет конечный предел для любого X из множества X при , то есть: 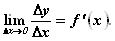По теореме, определяющей необходимое и достаточное условие существования предела, будем иметь: Где – бесконечно малая функция при , стремящемся к нулю. Находим приращение функции: Оно складывается из двух бесконечно малых функций при , поэтому их сумма бесконечно мала, что и доказывает непрерывность функции . Дифференцируемая функция непрерывна, значит, она имеет и предел в соответствующих точках.

43 Свойства дифференциала. Инвариантность формы дифференциала

Дифференциал обладает свойствами, аналогичными свойствам производной:

(С – постоянная величина) (8)

(9)

(10)

(11)

(12)

Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Рассмотрим дифференциал сложной функции. Пусть - сложная функция :

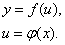
Дифференциал

этой функции, используя формулу для производной сложной функции, можно записать в виде

Но 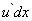есть дифференциал функции , поэтому

,

т.е.

(13)

Здесь дифференциал записан в том же виде, как и в формуле (7), хотя аргумент является не независимой переменной, а функцией . Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называют инвариантностью (неизменностью) формы дифференциала.

Подчеркнём, что в формуле (13) нельзя заменить на , так как

для любой функции , кроме линейной.

Не нашли, что искали? Воспользуйтесь поиском: