
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производные высших порядков
Если функция 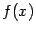 дифференцируема при всех
дифференцируема при всех  , то мы можем рассмотреть функцию
, то мы можем рассмотреть функцию 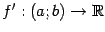 , сопоставляющую каждой точке
, сопоставляющую каждой точке 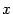 значение производной
значение производной 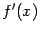 . Эта функция
. Эта функция  называется производной функции
называется производной функции 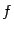 , или первой производной от
, или первой производной от 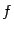 . (Иногда саму исходную функцию
. (Иногда саму исходную функцию 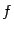 называют нулевой производной и обозначают тогда
называют нулевой производной и обозначают тогда  .) Функция
.) Функция 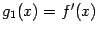 , в свою очередь, может иметь производную во всех (или некоторых) точках
, в свою очередь, может иметь производную во всех (или некоторых) точках 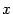 интервала
интервала 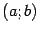 , которую мы обозначим
, которую мы обозначим  и назовём второй производной функции
и назовём второй производной функции 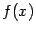 . Если предположить, что вторая производная
. Если предположить, что вторая производная  существует во всех точках
существует во всех точках  , то она может также иметь производную
, то она может также иметь производную 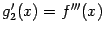 , называемую третьей производной функции
, называемую третьей производной функции 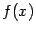 , и т. д. Вообще,
, и т. д. Вообще,  -й производной функции
-й производной функции 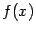 называется производная от предыдущей,
называется производная от предыдущей,  -й производной
-й производной 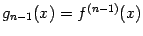 :
:
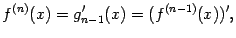
если эта производная существует.  -я производная называется также производной
-я производная называется также производной  -го порядка, а её номер
-го порядка, а её номер  называется порядком производной.
называется порядком производной.
При 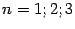 первую, вторую и третью производные принято обозначать штрихами:
первую, вторую и третью производные принято обозначать штрихами:  или
или 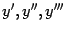 ; при прочих
; при прочих  -- числом в скобках в верхнем индексе:
-- числом в скобках в верхнем индексе: 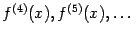 или
или 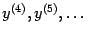 .
.
Физический смысл производной второго порядка проясняется из того, что если первая производная 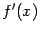 задаёт мгновенную скорость изменения значений
задаёт мгновенную скорость изменения значений 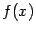 в момент времени
в момент времени 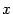 , то вторая производная, то есть производная от
, то вторая производная, то есть производная от 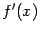 , задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений
, задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений 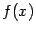 . Следовательно, третья производная -- это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения,
. Следовательно, третья производная -- это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения, 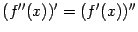 ).
).
Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.
Пример Найдём вторую производную функции  . Первая производная равна
. Первая производная равна
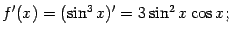
далее находим
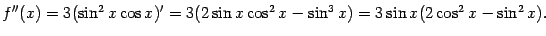
Пример 4.20 Пусть  . Тогда
. Тогда
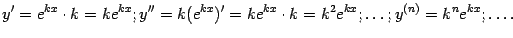
При 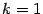 все производные оказываются равными исходной функции:
все производные оказываются равными исходной функции: 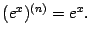
Пример Рассмотрим функцию  . Тогда
. Тогда
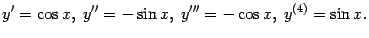
Поскольку четвёртая производная  совпала с исходной функцией
совпала с исходной функцией 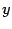 , то далее значения производных начнут повторяться с шагом 4: при
, то далее значения производных начнут повторяться с шагом 4: при  получаем
получаем

Заметим также, что
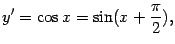
| |
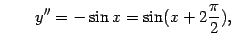
| |
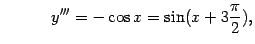
| |
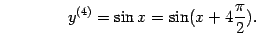
|
Легко видеть, что имеет место общая формула:
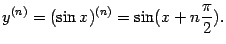
45 Теорема Ролля Пусть функция f: [ a, b ] → R непрерывна на сегменте [ a, b ], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f (a) = f (b). Тогда внутри сегмента [ a, b ] найдется точка ξ такая, что f' (ξ) = 0.
Теорема Ролля
Знание производной некоторой функции позволяет судить о характерных особенностях в поведении этой функции. В основе всех таких исследований лежат некоторые простые теоремы, называемые теоремами о среднем в дифференциальном исчислении.
Начнем рассмотрение таких теорем с теоремы, связываемой с именем французского математика Ролля (1652–1719).
Теорема 1.1. Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема во всех его внутренних точках, а на концах отрезка
, дифференцируема во всех его внутренних точках, а на концах отрезка  ,
,  обращается в ноль, то существует, по крайней мере, одна точка
обращается в ноль, то существует, по крайней мере, одна точка 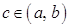 , в которой
, в которой 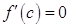 .
.
Доказательство. Так как функция непрерывна на отрезке  , то, согласно свойству 11.1.1, она должна достигать хотя бы один раз на этом отрезке своего минимума
, то, согласно свойству 11.1.1, она должна достигать хотя бы один раз на этом отрезке своего минимума 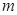 и максимума
и максимума 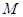 (рис. 1.1).
(рис. 1.1).
Если 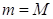 , функция постоянна, то есть
, функция постоянна, то есть 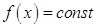 . Но в этом случае
. Но в этом случае 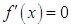 для любого
для любого 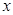 .
.
В общем случае 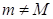 , и хотя бы одно из этих чисел не равно нулю. Предположим для определенности, что
, и хотя бы одно из этих чисел не равно нулю. Предположим для определенности, что 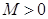 . Тогда существует точка
. Тогда существует точка 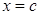 , в которой
, в которой 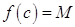 .
.

Рис. 1.1
Так как рассматриваемое значение 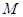 является максимальным, то для него справедливо, что
является максимальным, то для него справедливо, что  для
для 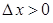 и
и 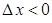 .
.
Рассмотрим пределы
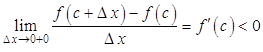 для
для 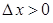
и
 для
для 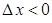 .
.
Так как оба предела равны производной функции  в одной и той же точке
в одной и той же точке 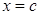 , то они равны между собой. Значит, из одновременности
, то они равны между собой. Значит, из одновременности 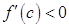 и
и 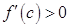 следует, что
следует, что 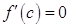 , что и требовалось доказать.
, что и требовалось доказать.
Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка  функция не обращается в ноль, но принимает равные значения
функция не обращается в ноль, но принимает равные значения 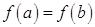 . Доказательство проводится аналогично.
. Доказательство проводится аналогично.
Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось  в двух точках
в двух точках  ,
,  или принимает в них равные значения, то, по крайней мере, в одной точке между
или принимает в них равные значения, то, по крайней мере, в одной точке между  и
и 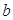 касательная к кривой параллельна оси
касательная к кривой параллельна оси  .
.
Необходимо отметить, что если не во всех точках  у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции
у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции 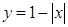 (рис. 1.2):
(рис. 1.2):

Рис. 1.2
Данная функция непрерывна на отрезке  и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.
и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.
46 Теорема Лагранжа Если функция f: [ a, b ] → R непрерывна на сегменте [ a, b ] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то 
 такое, что f (b) - f (a) = f' (ξ)(b - a). Теорема Лагранжа
такое, что f (b) - f (a) = f' (ξ)(b - a). Теорема Лагранжа
Результаты теоремы Ролля используются при рассмотрении следующей теоремы о среднем, принадлежащей Лагранжу (1736–1813).
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке 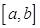 и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка
и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка 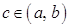 , в которой
, в которой 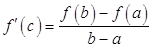 .
.
Доказательство. Рассмотрим график функции  (рис. 2.1).
(рис. 2.1).
Проведем хорду, соединяющую точки  и
и 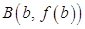 , и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:
, и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:
 ,
,
откуда:
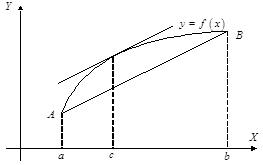
Рис. 2.1
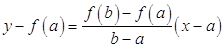 и
и 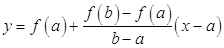 .
.
Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:
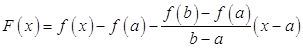 .
.
Полученная функция  непрерывна на отрезке
непрерывна на отрезке 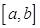 и дифференцируема во всех его внутренних точках. Кроме того, вычисление
и дифференцируема во всех его внутренних точках. Кроме того, вычисление  в точках
в точках  и
и  показывает, что
показывает, что 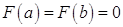 . Значит, функция
. Значит, функция  на отрезке
на отрезке  удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка
удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка 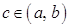 , в которой
, в которой 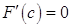 .
.
Вычислим производную функции  :
:
 .
.
Согласно теореме Ролля в точке 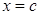 производная
производная 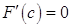 , то есть
, то есть  и
и
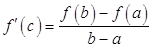 ,
,
что и требовалось доказать.
Геометрический смысл теоремы Лагранжа следующий: внутри отрезка  существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при
существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при 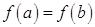 теорема переходит в теорему Ролля.
теорема переходит в теорему Ролля.
Теорему Лагранжа часто записывают в следующем виде:
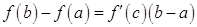 ,
,
то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.
47 Теорема Коши
Если каждая из функций f и g непрерывна на [ a, b ] и имеет конечную или бесконечную производную на ] a, b [ и если, кроме того, производная g' (x) ≠ 0 на ] a, b [, то 
 такое, что справедлива формула
такое, что справедлива формула 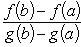
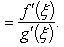 Если дополнительно потребовать, чтобы g (a) ≠ g (b), то условие g' (x) ≠ 0 можно заменить менее жестким:
Если дополнительно потребовать, чтобы g (a) ≠ g (b), то условие g' (x) ≠ 0 можно заменить менее жестким: 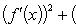
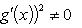

Теорема Коши
Рассмотрим, наконец, третью теорему о среднем, принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.
Теорема. Если функции 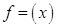 и
и 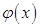 непрерывны на отрезке
непрерывны на отрезке  и дифференцируемы во всех его внутренних точках, причем
и дифференцируемы во всех его внутренних точках, причем  не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка
не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка 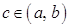 , в которой
, в которой 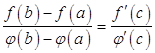 .
.
Доказательство. Так как  во всех точках
во всех точках  , то отсюда следует, что
, то отсюда следует, что 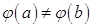 . В противном случае, как следует из теоремы Ролля, существовала хотя бы одна точка
. В противном случае, как следует из теоремы Ролля, существовала хотя бы одна точка 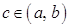 , в которой
, в которой  .
.
Составим вспомогательную функцию
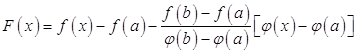 .
.
Данная функция непрерывна на отрезке  и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках
и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках  и
и  дает:
дает: 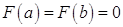 . Значит, функция
. Значит, функция  удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка
удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка 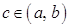 , в которой
, в которой 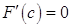 .
.
Вычислим производную  :
:
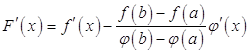 .
.
Из условия 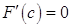 следует, что
следует, что
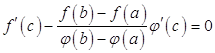 и
и 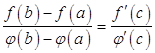 ,
,
что и требовалось доказать.
В случае, когда 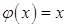 , теорема Коши переходит в формулировку теоремы Лагранжа.
, теорема Коши переходит в формулировку теоремы Лагранжа.
48 Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль 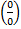 , бесконечность делить на бесконечность
, бесконечность делить на бесконечность  .К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность
.К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность 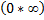 и бесконечность минус бесконечновть
и бесконечность минус бесконечновть  .
.
Вычислить предел, используя правило Лопиталя  Подставляем значение
Подставляем значение
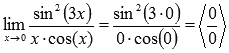
Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:

49 Найти предел 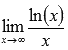 Подставляем бесконечность
Подставляем бесконечность 
Для данного типа неопределенностей можно использовать правило Лопиталя при нахождении предела. 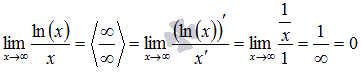
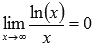
50 Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется Функцией двух переменных.
51 Пусть функция z = f (x,y) определена в точке M0(x0y0) и её окрестности.Функция называется непрерывной в точке M0(x0y0), если  Если функция f (x,y) непрерывна в точке M0(x0y0), тo
Если функция f (x,y) непрерывна в точке M0(x0y0), тo 
Поскольку 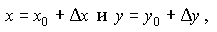
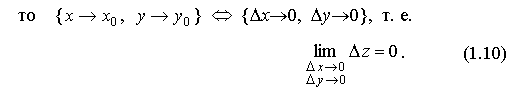
То есть, если функция f (x,y) непрерывна в точке M0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращение Δz функции z.
52 Свойства функций, непрерывных в ограниченной замкнутой области 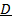 :
:
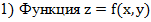 - является ограниченной в ограниченной замкнутой области
- является ограниченной в ограниченной замкнутой области 
2) 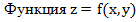 достигает в ограниченной замкнутой области
достигает в ограниченной замкнутой области  своих наибольшего и наименьшего значений.
своих наибольшего и наименьшего значений.
3)  принимает хотя бы в одной точке этой области любоt промежуточное значение между Х и У.
принимает хотя бы в одной точке этой области любоt промежуточное значение между Х и У.
53 частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
54
55 Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке 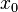 , а функция g имеет производную в точке
, а функция g имеет производную в точке 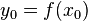 , то сложная функция h(x) = g(f(x)) также имеет производную в точке
, то сложная функция h(x) = g(f(x)) также имеет производную в точке 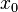 .
.
Не нашли, что искали? Воспользуйтесь поиском: