Тема 15. Функция случайной величины. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (НВС)

Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (НВС). Нормальное распределение.

14.1. Плотность распределения вероятностей НСВ Х имеет вид:

Сх², если – 1 х 1,

f (x)=

0, если |x|>1.

Найти: а) константу С; б) Р (Х 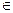[-2;0]); в) M[Х]; г) D[Х]; д) функцию распределения F(x).

14.2. Плотность распределения вероятностей НСВ Х имеет вид:

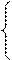0, если х [0; ],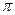

f (x)=

Csin x, если х 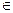[0; ].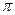

Найти: а) константу С; б) Р (Х 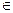[ 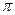/3; 5 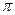/4]); в) M[Х]; г) функцию распределения F(x).

14.3. Плотность распределения вероятностей НСВ Х имеет вид:

0, если x<5,

f (x)=

C/x⁵, если х 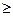5.

Найти: а) константу С; б) M[Х]; в) D[Х]; г) P(2<Х<10); д) функцию распределения F(x).

14.4. Плотность распределения вероятностей НСВ Х имеет вид:

0, если x<1,

f (x)=

C e^-2x, если х 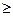1.

Найти: а) константу С; б) P (|X| 2); в) функцию распределения F(x).

14.5. Функция распределения НСВ Х имеет вид:

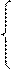1) 0, если x<2,

F (x)= (x – 2)², если 2 х 3

1, если x>3

2)

Найти: а) P (0,5 X 2,5); б) M[X]; в) D[X].

Законы распределения и числовые характеристики случайных векторов.

14.6. Дан закон распределения случайного вектора (X,Y) дискретного типа:

yj xi
- 1	0,1	0,05	0,05
	0,35	0,25	0,2

а) Найти: Р (Х= -1, Y=1), P(X=1, Y>0), P(X 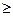Y), P(XY 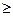0).

б) Найти безусловные законы распределения каждой из компонент случайного вектора (X,Y).

в) Выяснить, зависимы или нет случайные величины X и Y.

г) Построить условный закон распределения случайной величины Y при условии Х=1 и найти условное математическое ожидание M[Y/X=1].

д) Найти математическое ожидание случайного вектора (m_x, m_y), дисперсии D_X, D_Y каждой компоненты, ковариацию K_XY и коэффициент корреляции 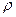_XY.

14.7. Дан закон распределения случайного вектора (X,Y):

yj xi
-1	0,3	0,12
	p	0,05
	0,35	0,03

Найти: р, Р (Х=0, Y=0), P(X Y), P(X 0, Y=1).

Выполнить задания б) – д) из предыдущей задачи для данного случайного вектора.

14.8. Дважды бросается игральная кость. Случайные величины: X – количество выпадений нечетного числа очков, Y – количество выпадений единицы. Построить закон распределения случайного вектора (X,Y). Найти Р(X Y). Выполнить задания б) – д) из задачи 3.8.1.

14.9. Один раз подбрасывается игральная кость. Случайные величины: Х – индикатор четного числа выпавших очков (Х=1, если выпало четное число, и Х=0 в остальных случаях), Y – индикатор числа очков, кратного трем (Y=1, если выпало число, кратное трем, и Y=0 в противном случае). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Зависимы или нет случайные величины Х и Y? Вычислить m_X, m_Y, D_X, D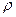_Y, _XY.

14.10. Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна 0,6. Случайные величины: Х – число промахов, Y – индикатор попадания при первом выстреле (Y=1, если при первом выстреле было попадание в мишень, и Y=0 в остальных случаях). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Вычислить m_X, m_Y, D_X, D_Y, 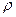_XY. Зависимы или нет случайные величины Х и Y?

14.11. Производится два независимых выстрела по цели с вероятностью попадания в цель, равной 0,6 при первом выстреле и 0,8 при втором. Случайные величины: Х – число попаданий при первом выстреле, Y – число попаданий при втором выстреле. Построить закон распределения случайного вектора (X,Y).

14.12. Из колоды в 36 карт наугад достают одну карту. Случайные величины: а) Х – число вынутых тузов, Y – число вынутых крестовых карт; б) Х – число вынутых тузов, Y – число вынутых карт-картинок. Построить закон распределения случайного вектора (X,Y). Найти коэффициент корреляции 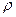_XY. Выяснить, зависимы Х и Y или нет.

пределения его компонент:

yj xi				P(X=xi)
		0,1	0,15	0,3
			0,3
P(Y=yj)	0,25

Заполнить пустые клетки в таблице. Найти m_X, m_Y, K_XY. Зависимы или нет Х и Y?

Литература:[2,3,4,7,16,17,19,21,23,24,25]

Учебно-методическая литература:[2]

Не нашли, что искали? Воспользуйтесь поиском: