Скалярное и векторное произведения векторов.

8.1. Векторы a и b образуют угол p/6, | а | = 2 и | b | = 5. Найти (a, b).

8.2. Векторы a и b образуют угол p/4, | а | = 4 и | b | = 3. Найти (a, b).

8.3. Векторы a и b образуют угол 2p/3, | а | = 3 и | b | = 2. Найти (a, b).

8.4. Векторы a и b образуют угол p/6, | а | = 2 и | b | = 1. Найти (2 a – 3 b, 4 a + 2 b).

8.5. Векторы a и b образуют угол p/4, | а | = 4 и | b | = 3. Найти (2 a – 3 b, a + 2 b).

8.6. Векторы a и b образуют угол 2p/3, | а | = 3 и | b | = 2. Найти (a –

3 b, 4 a + 2 b).

Прямая на плоскости.

8.7. Даны точки A = (1;2), B = (3;0), C = (6;2). Найти уравнение прямой, проходящей через точку A и параллельной вектору .

8.8. Даны точки A = (3;1), B = (1;-1), C = (0;2). Найти уравнение прямой, проходящей через точку A и параллельной вектору .

8.9. Найти уравнение прямой, проходящей через точки A = (1;2) и B = (3;8).

8.10. Найти уравнение прямой, проходящей через точки A = (1;2) и B = (3;4).

8.11. Найти уравнение прямой, проходящей через точки A = (-1;0) и B = (-1,3).

Плоскость.

8.12. Даны точка A = (1;-2;5) и вектор a = {-3,4,7}. Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору a.

8.13. Даны точки A = (1;2;0), B = (3,0,-3), C = (6,2,-2). Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору .

8.14. Даны точки A = (1;2;-1), B = (1,0,-1), C = (0,2,2). Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору .

8.15. Точка M₀ = (2;3;-1) – основание перпендикуляра, опущенного из точки A = (1;2;-1) на плоскость. Найти уравнение этой плоскости.

8.16. Точка M₀ = (3;4;-2) – основание перпендикуляра, опущенного из начала координат на плоскость. Найти уравнение этой плоскости.

Прямая в пространстве.

8.17. Даны точки A = (1;2;0), B = (3,0,-3), C = (6,2,-2). Найти канонические и параметрические уравнения прямой, проходящей через точку A и параллельной вектору .

8.18. Даны точки A = (1;2;-1), B = (1,0,-1), C = (0,2,2). Найти канонические и параметрические уравнения прямой, проходящей через точку A и параллельной вектору .

8.19. Даны точки A = (1;2;0) и B = (3,0,-3). Найти канонические и параметрические уравнения прямой, проходящей через точки A и B.

8.20. Даны точки A = (3;-2;1) и B = (5,0,2). Найти канонические и параметрические уравнения прямой, проходящей через точки A и B.

8.21. Даны точка A = (1;-3;2) и прямая 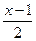L: = = . Найти канонические и параметрические уравнения прямой, проходящей через точку A и параллельной прямой L.

Литература:[1,4,6,9,10,12,13,14,15]

Учебно-методическая литература:[2]

Не нашли, что искали? Воспользуйтесь поиском: