Понятие о дифференциальных уравнениях. Уравнения 1-го порядка с разделяющимися переменными.

Уравнения 1-го порядка с разделяющимися переменными.

5.1. Выяснить, является ли функция у= решением дифференциального уравнения .

5.2. Выяснить, является ли функция решением дифференциального уравнения

5.3. Является ли функция решением дифференциального уравнения

5.4. Является ли функция решением дифференциального уравнения

Найти общий интеграл дифференциального уравнения:

5. Линейные дифференциальные уравнения 1-го порядка.

Найти общее решение дифференциального уравнения:

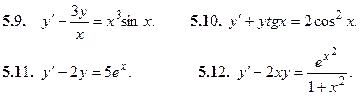
Литература:[1,4,6,9,10,12,13,14,15]

Учебно-методическая литература:[1]

Тема 6. Ряды

6.1. Понятие числового ряда. Необходимое условие сходимости ряда.

Ряды с неотрицательными членами. Признаки сходимости.

Вычислить первые четыре члена ряда:

Найти формулу для общего члена ряда:

Проверить, выполнено ли необходимое условие сходимости ряда:

Разложить функцию в ряд Маклорена и найти интервал сходимости полученного ряда.

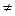6.21. f(x)= . 6.22. f(x)= a^x, a>0, a 1.

6.23. f (x)= sin 3x. 6.24. f(x)= e^-5x.

6.25. f(x)= cos x². 6.26. f(x)= .

6.27. f(x)= x³ e^5x. 6.28. f(x)= x²cos2x.

6.29. f(x)= sin² x. 6.30. f(x)= cos²x.

Литература:[1,4,6,9,10,12,13,14,15]

Учебно-методическая литература:[1]

Не нашли, что искали? Воспользуйтесь поиском: