Отображение. Функция.

Математика

Содержание

Глава 1. Элементы теории множеств.

1.1. Множества

1.2. Отношения

1.3. Отображения. Функции

Глава 2. Математическая логика.

2.1. Булевы функции

2.2. Логика предикатов

2.3. Решение логических задач с помощью булевых функций

Глава 3. Комбинаторика.

3.1. Общие правила комбинаторики

3.2. Перестановки

3.3. Размещения

3.4. Сочетания

Раздел 4. Элементы теории вероятностей.

4.1. Основные понятия

4.2. Определение вероятности события

4.3. Теорема сложения вероятностей

4.4. Теорема умножения вероятностей

Глава 5. Элементы теории графов.

5.1. Основные понятия теории графов.

5.2. Задача определения кратчайшего пути.

5.3. Задача о кратчайшем расстоянии между двумя пунктами.

5.4. Построение коммуникационной сети минимальной длины.

5.5. Задача определения максимального потока.

Глава 1. Элементы теории множеств

Множества

Теория множеств как математическая дисциплина создана немецким математиком Г.Кантором (1845-1918).

Множество – одно из основных (фундаментальных) понятий математики, а потому строгого определения не имеет. Описательно термин «множество» объясняется как собрание, совокупность, набор некоторых объектов произвольной природы, объединенных по каким-то общим для них признакам. Объекты, из которых состоит множество, называют его элементами.

Примеры множеств: все студенты университета, собрание книг в библиотеке, множество звезд Солнечной галактики, множество целых чисел и т.д.

Исходя из примеров, можно определить свойства множества:

1) элементы множества должны быть строго определены;

2) каждый элемент должен учитываться только один раз;

3) порядок расположения элементов внутри множества не имеет значения.

Пример: Множество студентов какой-либо группы университета.

Понятно, принадлежит студент данной группе или нет, в ведомости каждый учитывается только раз и порядок расположения фамилий не имеет значения.

Множества обозначают заглавными буквами латинского алфавита: A, B, C, D...; элементы – строчными: a, b, c,...

Символическая запись означает принадлежность элемента a множеству А. Запись означает, что элемент а не принадлежит множеству А.

Пример: Пусть А – множество четных чисел. Тогда , а .

Если число элементов множества конечно, то множество называют конечным, иначе – бесконечным. Считается, что примеры множеств, взятых из материального мира, конечны. Числовые множества – бесконечны.

Пример: Множество рыб в океане велико, но конечно. Множество действительных чисел – бесконечно.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .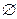

Существуют разные способы задания множеств. Конечное множество можно задать перечислением его элементов.

Пример: С= -- множество цифр десятичной системы счисления.

Также задать множество можно с помощью характеристического признака.

Пример: -- множество четных чисел.

Два множества равны, когда они состоят из одних и тех же элементов.

Пример: Множества 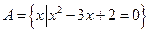и равны.

Пример: Множества и равны.

Множество А называют подмножеством множества В, если каждый элемент множества А является одновременно элементом множества В. В этом случае пишут 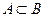(читается: «А включается или содержится в В»). Любое множество содержит 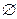в качестве подмножества. Очевидно, (записывают ); А и 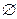называют несобственными подмножествами множества А. Все остальные подмножества называют собственными, т.е. кроме его элементов в множестве должен содержаться еще хотя бы один элемент.

Пример: Пусть , тогда .

Основные свойства включения: если ;

если -- равные множества.

Если все рассматриваемые множества, в ходе какого-либо рассуждения, являются подмножествами некоторого множества U, то это множество называют универсальным.

Пример: R – множество действительных чисел – универсальное множество, если в процессе изучения рассматриваются множества натуральных, целых и рациональных чисел

Существуют следующие операции над множествами:

1) объединение: -- элементы нового множества лежат хотя бы в одном из множеств А или В;

2) пересечение: 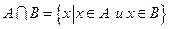-- элементы нового множества лежат в обоих множествах А; В;

3) разность: -- элементы нового множества – это элементы множества А, не содержащиеся в В;

4) дополнение множества А в множестве U (): .

Пример: .

Тогда .

Введенные операции обладают следующими свойствами:

(коммутативность).

(ассоциативность).

(дистрибутивность)

(идемпотентность).

(поглощение).

Задачи.

1. Используя диаграмму Венна, доказать законы 3 и 5.

2. Используя законы множеств, доказать равенства:

a) .

b) .

c) .

3. Заданы множества . Верным для них будет утверждение...

Варианты ответов:

a) «Множества А и В равны».

b) «Множество B есть подмножество множества A».

c) «Множество А есть подмножество множества В».

d) «Множества А и В не содержат одинаковых элементов».

4. Заданы произвольные множества А, В и С. Расположить указанные ниже четыре множества так, чтобы каждое из них было подмножеством следующего за ним:

a)

b)

c)

d) .

5. Даны множества . Установить соответствия между следующими множествами и их элементами:

6. Принято обозначать:

N – множество натуральных чисел;

Q – множество рациональных чисел;

Z – множество целых чисел;

R – множество действительных чисел.

Тогда верным утверждением будет...

Варианты ответов:

7. С помощью диаграмм Венна исследовать вопрос о справедливости каждого из следующих рассуждений:

а) если А, В, и С – такие подмножества множества U, что

;

b) если А, В, и С – такие подмножества множества U, что и , то .

Отношения.

Между элементами множеств можно установить отношения в виде их произведения. Декартовым произведением множеств А и В называют множество AxB всех упорядоченных пар элементов (а;b), где , т.е. . Элементы a и b при этом называют компонентами (координатами) пары.

Пример: . Тогда

.

Декартово произведение АxА называется декартовым квадратом множества А.

В целях наглядного представления декартовых произведений удобно использовать язык геометрии. Для этого множества X,Y представляются осями координат. Элементы -- соответственно абсциссами и ординатами. Само произведение -- точками плоскости XOY. Любое непустое подмножество такого произведения называется бинарным отношением. Ему можно придать прикладное значение. Например, значения множества X – названия предметов, изучаемых в университете, а элементы множества Y – группы студентов. Тогда отношению XxY можно придать смысл множества изучаемых студентами предметов.

По аналогии с декартовым произведением двух множеств X,Y можно построить декартово произведение XxYxZ трех и более множеств. Пример может быть следующий: по курсу x студент y выбрал билет z.

Бинарные отношения обладают следующими свойствами:

-- рефлексивность – отношение Р, при котором элемент отображается сам на себя, т.е. для любого x из Х выполняется xРx. Например, «x похож на x».

-- антирефлексивность – отношение, противоположное рефлексивности, т.е. xРx не выполняется ни для одного x из X. Например, «скорость компьютера x больше компьютера x». Данное отношение – скорость одного компьютера больше другого – обладает свойством антирефлексивности, т.к. скорость одного и того же компьютера не может превышать саму себя.

-- симметричность – отношение, при котором xРy влечет yРx. Например, отношение «x похож на y» обладает свойством симметричности, т.к. верно, что и «y похож на x». Отношение же «компьютер x быстрее y» не симметрично, т.к. «компьютер y быстрее x» уже не выполняется.

-- асимметричность – отношение, обратное симметричности, т.е. одно из двух соотношений xPy или yPx не выполняется. Отношение «компьютер x быстрее y» асимметрично.

-- антисимметричность – отношение, при котором xPy и yPx выполняются тогда и только тогда, когда x=y. Отношение «» выполняется только тогда, когда x=y.

-- транзитивность – отношение, при котором, из xPy и yPz следует xPz. Например, из того, что «студент В пришел позже студента А» и «студент С пришел позже студента В» следует, что «студент С пришел позже студента А».

Отношение Р называют отношением эквивалентности, если оно одновременно рефлексивно, транзитивно и симметрично.

Пример. Р – отношение равенства треугольников – отношение эквивалентности.

Отношение называют частичного (нестрогого) порядка, если оно одновременно рефлексивно, антисимметрично и транзитивно.

Пример. - рефлексивность

выполняются одновременно, когда 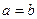- антисимметричность

Если , то 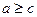- транзитивность.

Следовательно, отношение «» есть отношение частного порядка.

Отношение Р называют отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.

Пример. Отношение «<» на множестве чисел являются отношениями строгого порядка.

Задачи.

1. Заданы множества , тогда декартовым произведением этих множеств является множество...

Варианты ответов:

2. Выяснить, являются ли следующие отношения отношениями эквивалентности:

а) равенство в произвольной системе множеств;

b) отношение параллельности прямых;

с) отношение «проживания в одном доме» жителей города;

d) ;

e) .

3. Привести примеры отношений:

а) рефлексивного и симметричного, но не транзитивного в некотором множестве;

б) рефлексивного и транзитивного, но не симметричного;

в) симметричного и транзитивного, но не рефлексивного.

Отображение. Функция.

Понятие соответствия относится к первичным, неопределяемым понятиям математики. Говорят, что между двумя множествами установлено соответствие, если определено правило, по которому для каждого элемента одного множества выбирается определенный элемент или подмножество элементов другого множества. При этом допускается, что некоторым элементам первого множества может соответствовать пустое подмножество.

Пример. Пусть множество А – перечень размеров обуви от 35 до 45, В – множество студентов МГУКи. Тогда между А и В можно установить соответствие, при котором для каждого элемента А выбирается один, ни одного или совокупность(подмножество) элементов.

На основе понятия соответствия между множествами вводится понятие отображения множеств. При этом различают отображение множества «в» множество и отображение множества «на» множество.

Соответствие, при котором каждому элементу множества А отвечает единственный элемент множества В, называется отображением множества А в множество В.

Пример. Поставим в соответствие каждому слову некоторого словаря его заглавную букву. Такое соответствие определяет отображение множества слов словаря в множество букв алфавита.

Соответствие, при котором каждому элементу множества А отвечает единственный элемент множества В и, кроме того, каждому элементу множества В отвечает хотя бы один элемент множества А, называется отображением множества А на множество В.

Пример. Поставим в соответствие каждому трехзначному числу цифру его десятков. Такое соответствие определяет отображение множества трехзначных чисел на множество В= .

Отображения множеств обычно обозначают буквами f, g, h,…

и пишут .

Если при отображении f элементу соответствует элемент , то элемент b называют образом элемента а, элемент а называют прообразом элемента b и пишут.

.

Отображение f называют обратимым, если из условия вытекает , т.е. разным прообразам соответствуют разные образы. В этом случае каждый образ y имеет единственный прообраз x и можно определить отображение 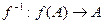, называемое обратным к отображению f. Обратное отображение устанавливает взаимно однозначное соответствие между множествами А и , т.е. такое соответствие, при котором каждому элементу множества А соответствует единственный элемент множества и каждому элементу множества соответствует единственный элемент множества А. Взаимно однозначное отображение называют также биекцией.

Отображение f называют функционалом, если множество В является множеством действительных чисел (B=R).

Пример. А – множество участков дорог на трассе. В – значения допустимой скорости.

Отображение f называют оператором. Если множества А и В – любой природы.

Пример. Каждому взрослому человеку соответствует свой ИНН.

Если же и множество А – числовое, то отображение f называют функцией. В частности, если , то говорят о функции одной переменной x. Множество принято обозначать и называть областью значений функции.

Пример. Элементарные функции являются числовыми функциями: .

Если (n-мерное пространство), то говорят о функции n переменных . В этом случае .

Задачи.

1. Изобразить отношение. Указать, является ли данное отношение функцией.

а) ;

б) ;

в) ;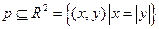

г) ;

д) .

2. Привести примеры функционала и оператора.

Не нашли, что искали? Воспользуйтесь поиском: