
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 5. Дифференциальные уравнения. 2.3. Пользуясь правилом дифференцирования сложной функции, найти производные функций:
2.3. Пользуясь правилом дифференцирования сложной функции, найти производные функций:
1) y=cos (x2 +2x - 4). 6) y=sin (x3 - 3x +5).
2) y=sin ex. 7) y=cos ln x.
3) y=e 2x-3. 8) y=e  .
.
4) y=etgx . 9) y=esinx.
5) y= ln(1+2 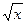 ). 10) y= ln(2x2 +4x -1).
). 10) y= ln(2x2 +4x -1).
2.4. Составить уравнения касательных к графикам функций:
1) y=x2 - 3x + 2 в точке (3;2).
2) y= 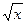 в точке (4;2).
в точке (4;2).
3) y= ln x в точке пересечения с осью Оx.
4) y= x2 - 5x + 6 в точках пересечения с осью Оx.
5) y=e7x в точке пересечения с осью Оy.
2.5. Найти дифференциалы функций:
1) y= x3 - 3ln x. 5) y= cos x  ex.
ex.
2) y= sin 3x. 6) y= tg ln x.
3) y= x2 arctg x. 7) y= 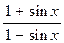 .
.
4) y=  . 8) y=
. 8) y= 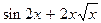 .
.
2.6. Найти приближенно приращение 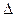 у:
у:
1) функции у= 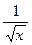 , если х= 4,
, если х= 4, 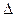 х= 0,08;
х= 0,08;
2) функции у= sinx, если х=  ,
, 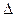 х= 0,02;
х= 0,02;
2.7. Найти дифференциалы 2-го порядка от функций:
1) y= x3 - 3x2 + x + 1. 3) y= (0,1x+1)5.
2) y= xcos2x. 4) y= sin2x.
2.8. Найти производные 3-го порядка от функций:
1) y=ex  cosx. 3) y= x2
cosx. 3) y= x2  ex.
ex.
2) y=ln(2x+5). 4) y= xlnx.
2.9. Найти производные n-го порядка от функций:
1) y=  . 3) y= e2x.
. 3) y= e2x.
2) y= 5x. 4) y= ln(1+x).
Правило Лопиталя.
2.10. Удовлетворяют ли условиям теоремы Ролля функции:
1) f(x)=x, x 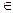 [0,1];
[0,1];
2) f(x)=  ;
;
2.11. Найти пределы с помощью правила Лопиталя:
1)  6)
6) 
2) 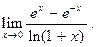 7)
7) 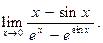
3)  8)
8) 
4)  9)
9) 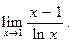
5) 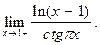 10)
10) 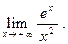
Исследование функций и построение графиков
2.11. Найти максимумы и минимумы и промежутки возрастания и убывания функций:
1) f(x)=x3 - 3x2 - 9x + 5; 2) f(x)= 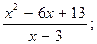
3) f(x)=xlnx; 4) f(x)= x - arctg2x;
3.1. Проверить, что:


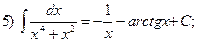
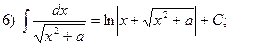
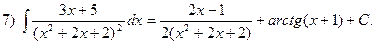
Литература: [№2,12,13].
Не нашли, что искали? Воспользуйтесь поиском: