
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
А) 150 мальчиков; б) от 150 до 200 мальчиков? 1.В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1
Вариант 7.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов  ,
, 
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 
 ,
,
если A1(2, - 2, 1), B1(1, 2, - 1), C1(1, 0, 2), D1(2, 1, 0).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а) все девушки оценят этот подарок; б) только одна девушка оценит этот подарок.
4. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно. что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,06 | p | 0,12 | 0,24 | 0,33 | 0,14 | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x2+2.
6. Вероятность нормального расхода электроэнергии за день на предприятии бытового обслуживания равна 0,7. Какова вероятность того, что из 90 дней предприятие нормально расходует электроэнергию: а) в течение 60 дней; б) от 60 до 90 дней?
Вариант 8.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов  ,
, 
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 
 ,
,
если A1(1, - 1, 1), B1(2, 1, - 1), C1(- 2, 0, 3), D1(2, - 2, - 4).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а) все монеты имеют нестандартный процент содержания золота; б) только одна монета имеет нестандартный процент содержания золота.
4. Магазин получил две равные по количеству партии одноименного товара. Известно что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,02 | 0,38 | 0,30 | p | 0,08 | 0,04 | 0,02 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью 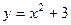 .
.
Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию а) 50 раз; б) от 100 до 150 раз?
Вариант 9.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов  ,
, 
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 
 ,
,
если A1(0, 1, - 1), B1(- 3, 0, 1), C1(1, 2, 0), D1(1, - 1, 2).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
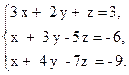
3. На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а) все выбранные булочки с изюмом; б) только одна булочка с изюмом.
4. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,08 | 0,10 | 0,14 | 0,17 | 0,19 | 0,18 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью 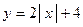
6. Установлено, что третья часть покупателей при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина: а) ровно 50 человек приобретут товар; б) от 100 до 120 человек приобретут товар?
7.2.4.Варианты контрольного задания для студентов заочной формы обучения всех специальностей (направлений) по прикладной математики (IV семестр)
Семестр.
Студенты, не получившие зачет по контрольной работе, не допускаются к сдаче экзамена по курсу.
Контрольная работа включает 5 задач в соответствии с табл. 1, по которой выбор из имеющихся 50 задач производится по первым буквам фамилии, имени и отчества студента. Так, например, студент Константинов Сергей Федорович должен выполнить следующие номера задач: 4,14, 28, 38,49.
Таблица 1.
| Первые буквы | Номера задач для контрольного задания | ||
| Фамилия МОП | Имя СМО ТИ | Отчество СПУ | |
| А | 1 11 | 21 31 | |
| Б В Г | 2 12 | 22 32 | |
| Д Е Ж | 3 13 | 23 33 | |
| З И К | 4 14 | 24 34 | |
| Л М | 5 15 | 25 35 | |
| Н О | 6 16 | 26 36 | |
| П Р | 7 17 | 27 37 | |
| С Т У | 8 18 | 28 38 | |
| ФХЦЧ | 9 19 | 29 39 | |
| ШЩЭЮЯ | 10 20 | 30 40 |
При выполнении контрольных работ необходимо соблюдать следующие правила:
1. Указать номера задач на обложке тетради.
2. Представлять решения задач подробно, последовательно с пояснением по этапам экономико-математического моделирования.
3. Сделать экономический анализ результатов решений в задачах.
4. Привести список используемых литературных источников в конце контрольной работы.
5. После получения отрецензированной работы студент должен сделать работу над ошибками и пройти собеседование.
ЗАДАЧИ
1. Построить экономико-математическую модель оптимизации плана хозяйственной деятельности предприятия розничной торговли, определить объем продажи товаров Хj по каждой товарной группе, обеспечивающие максимум торговой прибыли П при заданной величине товарооборота Qn с учетом следующих данных:
n - количество товарных групп;
j - номер товарной группы, j=1,2,3,...,n;
Pj - средняя розничная цена единицы товара j-ой группы, руб.
Xj - объем товарооборота j-й товарной группы;
Qпл - плановый объем товарооборота, руб.;
Сj - уровень издержек обращения в % к товарообороту j-й товарной группы;
 - уровень торговой скидки в % к товарообороту j-й товарной группы;
- уровень торговой скидки в % к товарообороту j-й товарной группы;
S - полезная площадь торговых залов, м2;
Sj - полезная площадь отдела, в котором продаются товары j- й товарной группы, м2;
q2j - норматив товарооборота j-й товарной группы на 1 м2 площади залов, руб/м2;
bl - рабочее время продавцов квалификации l, l=1,2,3,...,L;
qlj - норматив товарооборота по j-й товарной группе на группу продавцов квалификации l в единицу времени, руб./ч;
bh - издержки обращения по статье h, руб.;
qhj - плановый норматив издержек обращения по статье h, руб.;
h - номер статьи издержек обращения, h=1,2,3,...,H(h=1 зарплата, h=2 транспортные расходы и т.д.);
H - количество статей издержек обращения.
2. Построить экономико-математическую модель оптимизации плана хозяйственной деятельности предприятия розничной торговли, позволяющую определить товарооборот по каждой товарной группе Хj, обеспечивающий максимальный объем товарооборота Q при заданной величине торговой прибыли Ппл и условиях задачи № 1.
3. Торговое предприятие в течении месяца осуществляется реализацию n товарных групп (j=1,2,3,...,n), каждая из которых включает r видов товара (r=1,2,3,...,R). На реализацию товаров r-го вида каждой товарной j-ой группы заданы верхний gbjr и нижний gnjr пределы товарооборота. Предприятию установлен месячный план товарооборота Qпл тыс. руб. Построить экономико-математическую модель, позволяющую получить оптимальный месячный план продажи товаров  , обеспечивающий максимально торговую прибыль П при следующих условиях:
, обеспечивающий максимально торговую прибыль П при следующих условиях:
Sjr - площадь торговых залов на единицу товарооборота в натуральном выражении при реализации r вида товара из j-ой группы;
S - производственная площадь торгового предприятия, м2;
bl - месячный фонд времени работы продавцов квалификации l(l=1,2,3,...,L), чел./ч;
gljr - норматив товарооборота на группы продавцов квалификации l при реализации r-го вида товара из j-й группы в единицу времени;
Пjr - торговая прибыль от продажи единицы r-го вида товара из j-й группы, руб.;
Pjr - средняя розничная цена r-го вида товара из j-й группы, руб.;
bh - месячный лимит статьи h издержек обращения, h=1,2,3,...,H, руб.
qdjr - расходы по статье издержек обращения на 1 тыс. руб. товарооборота по реализации r-го вида товара из j-й группы, руб/тыс. руб.;
Qпл - плановый объем товарооборота.
4. Торговое предприятие в течение месяца осуществляется продажу n товарных групп, каждая из которых включает r видов товара (r=1,2,3,...,R). На реализацию товара r-го вида каждой товарной j-ой группы (j=1,2,3,...,n) заданы пределы товарооборота верхний gbjr и нижний gnjr. Построить экономико-математическую модель, позволяющую получить оптимальный месячный план продажи по каждому виду товара  , обеспечивающий при заданной величине торговой прибыли Ппл максимальный объем товарооборота Q по условиям задачи № 3.
, обеспечивающий при заданной величине торговой прибыли Ппл максимальный объем товарооборота Q по условиям задачи № 3.
5. Построить экономико-математическую модель организации снабжения товарами предприятий розничной торговой сети в городе, обеспечивающую минимум затрат на транспортные расходы С по завозу товаров при следующих условиях:
R - количество наименований товарных позиций;
r - номер наименования товара,(r=1,2,3,...,R);
m - количество розничных торговых предприятий;
i - номер розничного торгового предприятия, i=1,2,3,...,m;
n - количество оптовых торговых предприятий;
j - номер оптового торгового предприятия, j=1,2,3,...,n;
Зjr - запасы r-го товара на j-ом оптовом предприятии;
Mjr - объем реализации товара r-го наименования на i-м розничном предприятии;
Sr - спрос населения на товар r-го вида;
Cijr - стоимость перевозки единицы товара rиз j-го оптового торгового предприятия в i-е розничное;
Xijr - объем перевозок товаров r-го вида из j-го оптового в i-е розничное торговое предприятие.
6. Построить экономико-математическую модель организации снабжения товарами предприятий розничной торговли в городе, позволяющую получить максимальную прибыль по условиям задачи № 5.
7. Построить экономико-математическую модель развития предприятий розничной торговой сети в регионе, обеспечивающую минимум затрат на поездку жителей из населенных пунктов в торговые центры при следующих условиях:
n - число населенных пунктов;
j - номер населенного пункта, j=1,2,3,...,n;
Nj - численность населения j-го пункта;
m - количество торговых центров;
i - номер торгового центра, i=1,2,3,...,m;
Cij - затраты на поездку одного жителя из пункта j в пункт i торгового центра;
Xij - численность населения j-го пункта, обслуживаемого в i-ом центре;
R - количество наименований товарных позиций;
br - норма обеспеченности одного жителя товара, r-вида, r=1,2,3,...,R;
Mir - объем реализации товара r в i-м торговом центре;
Sj - спрос всего населения Nj в пункте j на товары.
8. Построить экономико-математическую модель развития предприятий розничной торговли в регионе, обеспечивающую получение максимальной торговой прибыли по условиям задачи
№7.
9. Построить экономико-математическую модель задачи размещения предприятий розничной торговли в регионе, имеющий n населенных пунктов, среди которых следует выбрать такие m, где следует расположить торговые центры, которые представляли бы населению соответствующие r товары в объеме br и ассортименте R, соответствующие нормам обеспеченности всего населения региона в целом S и при этом средневзвешенной затраты времени на поездку Т были бы минимальны, с учетом следующих данных:
R - количество наименований товарных позиций;
r - номер наименования товара,(r=1,2,3,...,R);
br - норма обеспеченности одного человека товарами r вида;
j - номер населенного пункта, j=1,2,3,...,n;
Nj - численность населения в j-м пункте;
Nmin - минимально допустимая численность населения, обслуживаемая торговым центром;
i - номер предприятия розничной торговли, i=1,2,3,...,m;
S - объем спроса на товары всего населения региона;
tij - затраты времени на поездку из j-го пункта до i-го торгового центра;
Tmax - максимально допустимые затраты времени на поездку до торгового центра;
Xij = 1, если i-й пункт прикреплен к i-му центру
0, в противоположном случае
10. Построить экономико-математическую модель задачи размещения предприятий розничной торговли, позволяющей минимизировать транспортные издержки на доставку товаров по условиям задачи № 9.
11. Построить экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальную прибыль на основе заданных нормативов в следующей таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-е молочные | 2-е прочие | ||
| Мясо, кг | 4,0 | 8,0 | - | - | 3,8 | |
| Рыба, кг | 2,5 | - | - | - | ||
| Овощи, кг | 3,2 | 2,0 | 3,0 | - | 4,6 | |
| Мука, крупа, макаронные изделия, кг | 2,1 | 2,6 | 2,3 | - | 2,8 | |
| Молоко, л | 6,5 | - | - | - | ||
| Прибыль, руб | 1,3 | 2,0 | 1,5 | 0,3 | 1,7 |
12. Построить экономико-математическую модель определения структуры блюд на предприятии общественного питания,
обеспечивающую максимальную прибыль на основе заданных нормативов в следующей таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-е молочные | 2-е прочие | ||
| Мясо, кг | 5,0 | 9,0 | - | - | 3,9 | |
| Рыба, кг | 3,0 | - | - | |||
| Овощи, кг | 3,4 | 5,0 | 3,5 | - | 4,7 | |
| Мука, крупа, макаронные изделия, кг | 2,7 | 2,8 | 2,5 | - | 2,9 | |
| Молоко, л | 6,4 | - | - | - | ||
| Прибыль, руб | 1,4 | 2,5 | 2,0 | 0,4 | 1,9 |
13. Построить экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальную прибыль на основе заданных нормативов в следующей таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-e молочные | 2-e прочие | ||
| Мясо, кг | 4,5 | 7,0 | - | - | 4,1 | |
| Рыба, кг | 3,5 | - | - | - | ||
| Овощи, кг | 3,3 | 4,0 | 3,3 | - | 4,9 | |
| Мука, крупа, макаронные изделия, кг | 2,5 | 2,7 | 2,4 | - | 3,1 | |
| Молоко, л | 6,3 | - | - | - | ||
| Прибыль, руб | 1,5 | 2,4 | 1,4 | 0,3 | 1,8 |
14. Построить экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальную прибыль на основе заданных
нормативов затрат продуктов на первые и вторые блюда, представленных в таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-e молочные | 2-e прочие | ||
| Мясо, кг | 4,2 | 7,8 | - | - | 3,6 | |
| Рыба, кг | 2,8 | - | - | - | ||
| Овощи, кг | 3,4 | 2,9 | 3,2 | - | 4,7 | |
| Мука, крупа, макаронные изделия, кг | 2,7 | 2,6 | 2,8 | - | 2,7 | |
| Молоко, л | 6,8 | - | - | - | ||
| Прибыль, руб | 1,8 | 2,2 | 1,5 | 0,25 | 1,8 |
15. Построить экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальную прибыль на основе заданных нормативов затрат ресурсов на первые и вторые блюда, представленных в таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-е молочные | 2-e прочие | ||
| Затраты труда на производство, чел./ч. | 3,4 | 5,0 | 38,0 | 2,6 | ||
| Затраты труда на обслуживание, чел./ч. | 2,1 | 5,2 | 5,1 | 2,8 |
Продолжение табл.
| Издержки производства и обращения, у.е. | 4,3 | 6,9 | 6,7 | 4,1 | ||
| Прибыль, у.е. | 1,3 | 2,0 | 1,5 | 0,3 | 1,7 | |
| Товарооборот, у.е. |
16. Построить экономико-математическую модель определения структуры выпуска первых и вторых блюд на предприятии общественного питания при заданном квартальном плане товарооборота и получении максимальной прибыли на основе данных, приведенных в следующей таблице:
| Ресурсы | Плановый фонд ресурсов | Нормативы затрат ресурсов на 100 блюд | ||||
| 1-е блюдо | 2-е мясные | 2-е рыбные | 2-е молочные | 2-e прочие | ||
| Затраты труда на производство, чел./ч. | 3,6 | 6,0 | 37,0 | 2,5 | ||
| Затраты труда на обслуживание, чел./ч. | 2,2 | 5,3 | 5,2 | 2,7 | 3.1 | |
| Издержки производства и обращения, у.е. | 4,4 | 6,7 | 6,8 | 4,2 | ||
| Прибыль, у.е. | 1,4 | 2,1 | 1,6 | 0,31 | 1,8 | |
| Товарооборот, у.е. |
17. Построить экономико-математическую модель определения структуры товарооборота розничного предприятия торговли при заданных затратах ресурсов на единицу товарооборота, объемах ресурсов и установленном товарообороте на плановый период с объемом 300000 у.е., представленных в следующей таблице:
| Показатели | Товарная группа, затраты на 1 т | Объем ресурсов | ||
| мясо | колбас. изделия | масло живот., сыр | ||
| Фонд рабочего времени, чел./ч | ||||
| Площадь торговых залов, м2 | 3,5 | |||
| Издержи обращения, у.е. | ||||
| Среднегрупповая цена реализации за 1 т, у.е. | ||||
| Прибыль от продажи 1т, у.е. |
18. Построить экономико-математическую модель определения структуры товарооборота розничного предприятия торговли при заданных затратах ресурсов на единицу товарооборота, объемах ресурсов и установленном товарообороте на плановый период с объемом 300000 у.е., представленных в следующей таблице:
| Показатели | Товарная группа, затраты на 1 т | Объем ресурсов | ||
| мясо | колбас. изделия | масло живот., сыр | ||
| Фонд рабочего времени, чел./ч | ||||
| Площадь торговых залов, м2 | 2,1 | 3,2 | 3,6 | |
| Издержи обращения, у.е. |
Продолжение табл.
| Среднегрупповая цена реализации за 1 т, у.е. | ||||
| Прибыль от продажи 1т, у.е. |
19. Построить экономико-математическую модель определения структуры товарооборота розничного предприятия торговли при заданных затратах ресурсов на единицу товарооборота, объемах ресурсов и установленном товарообороте на плановый период с объемом 300000 у.е., представленных в следующей таблице:
| Показатели | Товарная группа, затраты на 1 т | Объем ресурсов | ||
| мясо | колбас. изделия | масло живот., сыр | ||
| Фонд рабочего времени, чел./ч | ||||
| Площадь торговых залов, м2 | 2,2 | 3,1 | 3,7 | |
| Издержи обращения, у.е. | ||||
| Среднегрупповая цена реализации за 1 т, у.е. | ||||
| Прибыль от продажи 1т, у.е. |
20. Построить экономико-математическую модель определения структуры товарооборота розничного предприятия торговли при заданных затратах ресурсов на единицу товарооборота, объемах ресурсов и установленном товарообороте на плановый период с объемом 300000 у.е., представленных в следующей таблице:
| Показатели | Товарная группа, затраты на 1 т | Объем ресурсов | ||
| мясо | колбас. изделия | масло живот., сыр | ||
| Фонд рабочего времени, чел./ч | ||||
| Площадь торговых залов, м2 | 2,5 | 3,0 | 3,2 | |
| Издержи обращения, у.е. | ||||
| Среднегрупповая цена реализации за 1 т, у.е. | ||||
| Прибыль от продажи 1т, у.е. |
21.-22. На оптовую базу прибывают автомашины с промышленными товарами. Поток простейших и поступает с интенсивностью  автомашин в час. На территории базы могут одновременно находится не более m автомашин. Имеющиеся на базе n бригад грузчиков разгружают одновременно все только одну машину. Среднее время разгрузки одной машины составляет
автомашин в час. На территории базы могут одновременно находится не более m автомашин. Имеющиеся на базе n бригад грузчиков разгружают одновременно все только одну машину. Среднее время разгрузки одной машины составляет  . Необходимо определить основные показатели СМО оптовой базы при следующих значениях исходных данных:
. Необходимо определить основные показатели СМО оптовой базы при следующих значениях исходных данных:
21) n=1 m=3 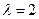 авт./ч.
авт./ч. 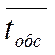 =1,5 ч.
=1,5 ч.
22) n=2 m=3  авт./ч.
авт./ч.  =1ч.
=1ч.
23.-25. Универсам получает ранние овощи и зелень из теплиц пригородного совхоза. Машины с товаром прибывают в универсам в неопределенное время. В среднем прибывает  автомашин в день. Подсобные помещения и оборудование для подготовки овощей к продаже позволяют обработать и хранить товар объемом не более m автомашин одновременно. В универсаме работают n фасовщиков, каждый из которых в среднем может обработать товар с одной автомашины в течение tобс.дня. Определить вероятность обслуживания приходящей автомашины Робс. Какова должна быть емкость подсобных помещений m1, чтобы вероятность обслуживания была бы больше или равна заданной величине, т.е.
автомашин в день. Подсобные помещения и оборудование для подготовки овощей к продаже позволяют обработать и хранить товар объемом не более m автомашин одновременно. В универсаме работают n фасовщиков, каждый из которых в среднем может обработать товар с одной автомашины в течение tобс.дня. Определить вероятность обслуживания приходящей автомашины Робс. Какова должна быть емкость подсобных помещений m1, чтобы вероятность обслуживания была бы больше или равна заданной величине, т.е.  :
:
23)  =3авт.день
=3авт.день  =0,5 дня n=2 m=2 Р*обс.=0,92
=0,5 дня n=2 m=2 Р*обс.=0,92
24)  =3авт.день
=3авт.день  =0,3 дня n=2 m=2 Р*обс.=0,97
=0,3 дня n=2 m=2 Р*обс.=0,97
25)  =6авт.день
=6авт.день  =0,25 дня n=4 m=2 Р*обс.=0,93
=0,25 дня n=4 m=2 Р*обс.=0,93
26.-28. В магазин самообслуживания поступает пуассоновский поток покупателей с интенсивностью 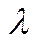 человек в минуту. Средняя продолжительность обслуживания на расчетном узле составляет
человек в минуту. Средняя продолжительность обслуживания на расчетном узле составляет  мин. Уровень суммарных потерь связан с простоем среднего числа свободных контролеров-кассиров
мин. Уровень суммарных потерь связан с простоем среднего числа свободных контролеров-кассиров  и пребыванием среднего числа покупателей в очереди lоч. Построить график зависимости суммы среднего числа свободных контролеров-кассиров
и пребыванием среднего числа покупателей в очереди lоч. Построить график зависимости суммы среднего числа свободных контролеров-кассиров  и среднего
и среднего  числа покупателей в очереди от числа контролеров-кассиров n, (
числа покупателей в очереди от числа контролеров-кассиров n, ( +
+ 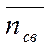 )=f(n). Определить по нему оптимальное число контролеров-кассиров n0, при котором суммарные потери будут минимальными.
)=f(n). Определить по нему оптимальное число контролеров-кассиров n0, при котором суммарные потери будут минимальными.
26) 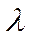 =1,0 пок./мин
=1,0 пок./мин  =2 мин.
=2 мин.
27)  =2,0 пок./мин
=2,0 пок./мин  =1,4 мин.
=1,4 мин.
28)  =0,5 пок./мин
=0,5 пок./мин  =1,8 мин.
=1,8 мин.
29.-30. В магазин самообслуживания поступает пуассоновских поток с интенсивностью  покупателей в час. В течение дня их обслуживают n контролеров-кассиров с интенсивностью
покупателей в час. В течение дня их обслуживают n контролеров-кассиров с интенсивностью  покупателей в час. Интенсивность входного потока покупателей в часы “пик” возрастает до величины
покупателей в час. Интенсивность входного потока покупателей в часы “пик” возрастает до величины 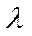 max, а в часы “спада” достигает величины
max, а в часы “спада” достигает величины 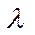 min. Определить вероятность образования очереди в магазине Роч и среднюю длину очереди lоч в течение дня, а затем необходимое число контролеров-кассиров в часы “пик” nmax и часы “спада nmin, обеспечивающих такую же длину очереди lоч и вероятность ее образования Роч.
min. Определить вероятность образования очереди в магазине Роч и среднюю длину очереди lоч в течение дня, а затем необходимое число контролеров-кассиров в часы “пик” nmax и часы “спада nmin, обеспечивающих такую же длину очереди lоч и вероятность ее образования Роч.
29) 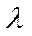 =200 пок./ч.
=200 пок./ч. 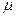 =90 пок./ч n=3
=90 пок./ч n=3  max=400 пок./ч.
max=400 пок./ч.
 min=100 пок./ч.
min=100 пок./ч.
30)  =300 пок./ч.
=300 пок./ч. 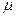 =120 пок./ч n=3
=120 пок./ч n=3  max=500 пок./ч.
max=500 пок./ч.
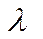 min=140 пок./ч.
min=140 пок./ч.
31.-32. Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.
3.1.
 0,7
0,7
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| К1 | К2 | К3 | К4 | |
| П1 | 5,0 | 4,5 | 5,1 | 4,0 |
| П2 | 4,2 | 5,6 | 3,9 | 4,3 |
| П3 | 3,6 | 4,1 | 4,7 | 4,0 |
| П4 | 3,5 | 3,9 | 4,6 | 3,8 |
3.2.
 0,6
0,6
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| К1 | К2 | К3 | К4 | |
| П1 | ||||
| П2 | ||||
| П3 | ||||
| П4 |
3.3.-3.5. Экономисты оптового торгового предприятия на основе возможных вариантов поведения поставщиков П1,П2,П3,П4, разработали несколько своих хозяйственных планов О1, О2, О3, О4, а результаты всех возможных исходов представили в виде матрицы прибыли (выигрышей). Определить оптимальный план оптового торгового предприятия.
3.3.
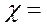 0,8
0,8
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| П1 | П2 | П3 | П4 | |
| О1 | 2,3 | 3,4 | 3,0 | 3,4 |
| О2 | 3,0 | 2,9 | 2,6 | 3,7 |
| О3 | 2,8 | 3,8 | 3,6 | 3,0 |
| О4 | 4,0 | 2,9 | 4,0 | 4,2 |
3.4.
 0,7
0,7
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| П1 | П2 | П3 | П4 | |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
3.5.
 0,6
0,6
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| П1 | П2 | П3 | П4 | |
| О1 | 0,8 | 1,4 | 3,2 | 2,6 |
| О2 | 4,2 | 0,1 | 1,6 | 2,2 |
| О3 | 2,6 | 3,8 | 0,2 | 0,4 |
| О4 | 1,4 | 4,0 | 2,0 | 5,2 |
3.6.-3.7. Розничное предприятие торговли формирует заявку на новые товары Н1, Н2, Н3, заменяющие старые товары, хорошо известные покупателям. Методы изучения спроса позволили составить матрицу условных вероятностей 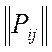 продажи старых товаров С1, С2, С3, при наличии конкурирующих новых товаров в торговой сети.
продажи старых товаров С1, С2, С3, при наличии конкурирующих новых товаров в торговой сети.
Составить план-заказ на товары, чтобы обеспечить оптимальное соотношение между их продажей.
36.
| Старые товары | Новые товары | ||
| Н1 | Н2 | Н3 | |
| С1 | 0,6 | 0,3 6 | 0,1 |
| С2 | 0,2 | 0,7 | 0,1 |
| С3 | 0,1 | 0,4 5 | 0,5 |
37.
| Старые товары | Новые товары | ||
| Н1 | Н2 | Н3 | |
| С1 | 0,7 | 0,1 7 | 0,2 |
| С2 | 0,6 | 0,2 | 0,2 |
| С3 | 0,6 | 0,3 3 | 0,1 |
38.- 40. Предприятие общественного питания планирует выпуск трех партий новых, ранее не производимых полуфабрикатов П1, П2, П3, в условиях неясной рыночной конъюнктуры, относительно которой известны лишь отдельные возможные состояния Р1, Р2, Р3, Р4, а также возможные объемы товарооборота по каждому варианту, и их условные вероятности, которые представлены в виде Рij матрицы. Определить предпочтительный план выпуска полуфабрикатов.
38.
| Партии полуфабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 0,4 2,2 | 0,1 3,8 | 0,2 2,8 | 0,3 3,2 |
| П2 | 0,3 2,6 | 0,2 2,4 | 0,1 3,1 | 0,4 3,3 |
| П3 | 0,2 3,0 | 0,3 2,0 | 0,2 1,8 | 0,3 2,5 |
39.
| Партии полуфабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 0,2 2,4 | 0,3 0,9 | 0,2 1,7 | 0,3 1,2 |
| П2 | 0,3 1,4 | 0,2 1,8 | 0,1 1,3 | 0,4 1,6 |
| П3 | 0,4 1,2 | 0,1 2,0 | 0,2 1,8 | 0,3 1,3 |
40.
| Партии полуфабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 0,3 1,2 | 0,2 2,1 | 0,1 1,7 | 0,4 2,0 |
| П2 | 0,4 1,5 | 0,1 1,3 | 0,2 1,6 | 0,3 1,8 |
| П3 | 0,2 1,7 | 0,3 1,6 | 0,2 1,9 | 0,3 1,4 |
41.-50. Даны упорядоченная структурно-временная табл.10. перечня работ по организации выставки продажи товаров. Требуется построить сетевой график, определить критический путь, критические работы, резервы времени, провести графический анализ комплекса работ и оптимизацию сетевой модели по критерию минимума времени Т при заданных ресурсах В. Определить экономию. Построить оптимальный сетевой план работ.
Таблица 10.
| Содержание работы | Обозначение, аi | Опорные работы,аj | Коэф Пересчета, сi=1/bi | Длительность работы, ч | |||||
| Обознач. ti | Номер задачи | ||||||||
| Заказ на оборудование и товары | а1 | - | с1=0,1 | t1= | |||||
| Разработка системы учета спроса | а2 | - | с2=0,2 | t2= | |||||
| Отбор товаров и выписка счетов | а3 | а1 | с3=0,3 | t3= | |||||
| Завоз товара | а4 | а3 | с4=0,4 | t4= | |||||
| Завоз оборудования | а5 | а1 | с5=0,5 | t5= | |||||
| Установка оборудования | а6 | а5 | с6=0,6 | t6= | |||||
| Выкладка товара | а7 | а4 | с7=0,7 | t7= | |||||
| Учет наличия товара | а8 | а4 | с8=0,8 | t8= | |||||
| Оформление зала и витрины | а9 | а6а7 | с9=0,9 | t9= | |||||
| Изучение документов учета | а10 | а2 а8 | С10=1,0 | t10= | |||||
| Репетиция выставки продажи | а11 | а9а10 | с11=1,1 | t11= |
| Содержание работы | Обозначение, аi | Опорные работы,аj | Коэф Пересчета, сi=1/bi | Длительность работы, ч | Оптим t0i | ||||||||||
| Обознач. ti | Номер задачи | ||||||||||||||
| Заказ на оборудование и товары | а1 | - | с1= | t1= | ? | ||||||||||
| Разработка системы учета спроса | а2 | - | с2= | t2= | ? | ||||||||||
| Отбор товаров и выписка счетов | а3 | а1 | с3= | t3= | ? | ||||||||||
| Завоз товара | а4 | а3 | с4= | t4= | ? | ||||||||||
| Завоз оборудования | а5 | а1 | с5= | t5= | ? | ||||||||||
| Установка оборудования | а6 | а5 | с6= | t6= | ? | ||||||||||
| Выкладка товара | а7 | а4 | с7= | t7= | ? | ||||||||||
| Учет наличия товара | а8 | а4 | с8= | t8= | ? | ||||||||||
| Оформление зала и витрины | а9 | а6а7 | с9= | t9= | ? | ||||||||||
| Изучение документов учета | а10 | а2 а8 | с10= | t10= | ? | ||||||||||
| Репетиция выставки продажи | а11 | а9а10 | с11=1,1 | t11= | ? | ||||||||||
ПРАВИЛА ОФОРМЛЕНИЯ РАБОТЫ
На титульном листе тетради должны быть написаны наименование дисциплины, наименование факультета, курс, фамилия, имя, отчество.
В начале работы или на титульном листе должны быть указаны номера задач, выполненных в контрольном задании.
Перед решением каждой задачи надо полностью записать ее условие. Решение задач должно включать развернутые расчеты и краткие пояснения, экономический анализ полученных результатов. В конце контрольной работы привести список использованной литературы и поставить свою подпись.
В процессе выполнения контрольной работы студент может получить на кафедре устную или письменную консультацию.
Допущенную к защите контрольную работу вместе с рецензией на нее студент должен представить на собеседование.
Студент, не выполнивший контрольную работу и не прошедший собеседование, к экзамену не допускается.
Не нашли, что искали? Воспользуйтесь поиском: