
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Законы распределения и числовые характеристики случайных векторов.
4.48. Дан закон распределения случайного вектора (X,Y) дискретного типа:
| yj xi | |||
| - 1 | 0,1 | 0,05 | 0,05 |
| 0,35 | 0,25 | 0,2 |
а) Найти: Р (Х= -1, Y=1), P(X=1, Y>0), P(X  Y), P(XY
Y), P(XY  0).
0).
б) Найти безусловные законы распределения каждой из компонент случайного вектора (X,Y).
в) Выяснить, зависимы или нет случайные величины X и Y.
г) Построить условный закон распределения случайной величины Y при условии Х=1 и найти условное математическое ожидание M[Y/X=1].
д) Найти математическое ожидание случайного вектора (mx, my), дисперсии DX, DY каждой компоненты, ковариацию KXY и коэффициент корреляции  XY.
XY.
4.49. Дан закон распределения случайного вектора (X,Y):
 yj
xi yj
xi
| ||
| -1 | 0,3 | 0,12 |
| p | 0,05 | |
| 0,35 | 0,03 |
Найти: р, Р (Х=0, Y=0), P(X  Y), P(X
Y), P(X  0, Y=1).
0, Y=1).
Выполнить задания б) – д) из предыдущей задачи для данного случайного вектора.
Дважды бросается игральная кость. Случайные величины: X – количество выпадений нечетного числа очков, Y – количество выпадений единицы. Построить закон распределения случайного вектора (X,Y). Найти Р(X Y). Выполнить задания б) – д) из задачи3.8.1.
4.51. Один раз подбрасывается игральная кость. Случайные величины: Х – индикатор четного числа выпавших очков (Х=1, если выпало четное число, и Х=0 в остальных случаях), Y – индикатор числа очков, кратного трем (Y=1, если выпало число, кратное трем, и Y=0 в противном случае). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Зависимы или нет случайные величины Х и Y? Вычислить mX, mY, DX, DY,  XY.
XY.
4.52. Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна 0,6. Случайные величины: Х – число промахов, Y – индикатор попадания при первом выстреле (Y=1, если при первом выстреле было попадание в мишень, и Y=0 в остальных случаях). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Вычислить mX, mY, DX, DY,  XY. Зависимы или нет случайные величины Х и Y?
XY. Зависимы или нет случайные величины Х и Y?
4.53. Производится два независимых выстрела по цели с вероятностью попадания в цель, равной 0,6 при первом выстреле и 0,8 при втором. Случайные величины: Х - число попаданий при первом выстреле, Y – число попаданий при втором выстреле. Построить закон распределения случайного вектора (X,Y).
4.54. Из колоды в 36 карт наугад достают одну карту. Случайные величины: а) Х – число вынутых тузов, Y – число вынутых крестовых карт; б) Х – число вынутых тузов, Y – число вынутых карт-картинок. Построить закон распределения случайного вектора (X,Y). Найти коэффициент корреляции  XY. Выяснить, зависимы Х и Y или нет.
XY. Выяснить, зависимы Х и Y или нет.
Тема 11. Вариационный ряд и его характеристики. Выборочный метод. Статистические оценки параметров распределений: точечные и интервальные оценки. Проверка статистических гипотез. Элементы регрессионного анализа.
5.1. Из генеральной совокупности, распределенной по нормальному закону, сделана выборка. Найти: 1) числовые характеристики выборки – выборочную среднюю, выборочную дисперсия, выборочное среднее квадратическое отклонение; 2) несмещенные оценки для генеральной средней и генеральной дисперсии; 3) доверительный интервал для оценки генеральной средней с заданной надежностью γ.
Вариант 1.

| 54-58 | 58-62 | 62-66 | 66-70 | 70-74 | 74-78 | 78-82 |

|
 .
.
Вариант 2

| 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |

|
 .
.
Вариант 3.

| 0-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 |

|
 .
.
Вариант 4.

| 33,2 | 38,2 | 43,2 | 48,2 | 53,2 |

|
 .
.
Вариант 5.

| 15,4 | 18,4 | 21,4 | 24,4 | 27,4 |

|
 .
.
Вариант 6.

| ||||||

|
 .
.
Вариант 7.

| 4 - 9 | 9 - 14 | 14 - 19 | 19 - 24 | 24 - 29 |

|
 .
.
5.2. Имеются две нормально распределенные генеральные совокупности  и
и  , из которых были сделаны выборки. По полученным выборкам на уровне значимости
, из которых были сделаны выборки. По полученным выборкам на уровне значимости  проверить гипотезу
проверить гипотезу 
 , считая дисперсии неизвестными, но равными.
, считая дисперсии неизвестными, но равными.
Вариант 1.

| |||||||

|
Уровень значимости  , альтернативная гипотеза
, альтернативная гипотеза 

Вариант 2.

| |||||||

|
Уровень значимости  , альтернативная гипотеза
, альтернативная гипотеза 

Вариант 3.

| |||||||

|
Уровень значимости  , альтернативная гипотеза
, альтернативная гипотеза 

5.3. Была исследована зависимость признака  от признака
от признака  . В результате проведения 10 измерений были получены результаты, представленные в таблице.
. В результате проведения 10 измерений были получены результаты, представленные в таблице.
Требуется: 1) оценить тесноту и направление связи между признаками с помощью коэффициента корреляции и оценить значимость коэффициента корреляции на уровне значимости  ; 2) найти уравнение линейной регрессии
; 2) найти уравнение линейной регрессии  на
на  ; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.
; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.
Вариант 1.

| ||||||||||

|
Уровень значимости 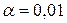 .
.
Вариант 2.

| 6,0 | 6,5 | 6,8 | 7,0 | 7,4 | 8,0 | 8,2 | 8,7 | 9,0 | 10,0 |

|
Уровень значимости  .
.
Вариант 3.

| 39,0 | 38,7 | 38,9 | 40,1 | 39,4 | 39,4 | 39,5 | 39,1 | 40,4 | 39,5 |

|
Уровень значимости  .
.
Вариант 4.

| ||||||||||

|
Уровень значимости  .
.
Не нашли, что искали? Воспользуйтесь поиском: