Оборудование и технологии высокоэффективных процессов обработки материалов;

Контрольная работа №2 по математике

Для студентов 1 курса заочного отделения

факультета инновационных технологий в машиностроении специальностей:

Техническая эксплуатация автомобилей;

оборудование и технологии высокоэффективных процессов обработки материалов;

(2-ой семестр)

Изучаемые разделы: Элементы высшей алгебры. Комплексные числа. Интегральное исчисление функций одной переменной. Дифференциальное исчисление функций многих переменных. Интегральное исчисление функций многих переменных. Векторный анализ и элементы теории поля.

1.Решение типового варианта.

Задача 1. Заданы два комплексных числа и . Вычислить + , - , * , / . Найти модуль и аргумент комплексного числа и изобразить его на плоскости, записать число в тригонометрической и показательной форме, вычислить .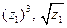

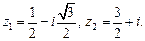
Решение.

По формулам суммы, разности и произведения комплексных чисел имеем

+ =

- =

* =

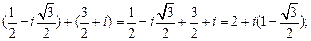
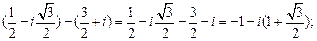
Для вычисления частного умножим числитель и знаменатель дроби на число сопряженное знаменателю и выполним преобразования

По формулам для определения модуля r и аргумента 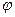комплексного числа находим,

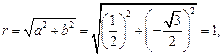
Тогда 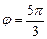. Это означает, что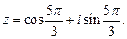

Показательная форма записи числа имеет вид

Изобразим на плоскости комплексное число

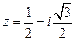
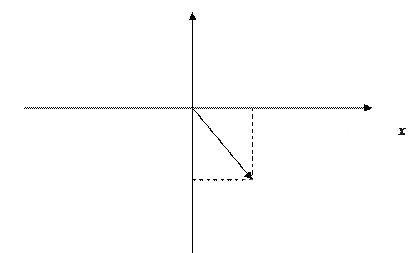
Для возведения комплексного числа в степень удобно воспользоваться формулой Муавра в тригонометрической или показательной форме.

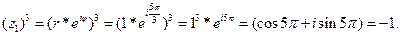
Корень n -ой степени из комплексного числа z имеет n значений 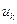, k =0,1,…, n -1, которые находятся по формулам

- арифметический корень n -ой степени из r. Используя эти формулы, получаем

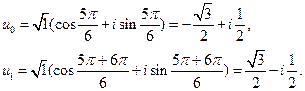
Задача 2. Используя ортогональное преобразование, привести к каноническому виду уравнение кривой 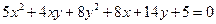и найти формулы преобразования координат.

Решение. Обозначим .

Матрица этой квадратичной формы имеет вид .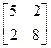

Составим характеристическое уравнение матрицы

.

Откуда .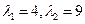

Найдем собственные векторы.Для 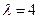имеем систему уравнений

.

Тогда .

Нормируя полученные векторы, находим

.

Для 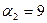получаем систему

.

Следовательно, .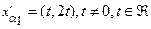

Нормируя полученные векторы, имеем

.

Таким образом, матрица преобразования координат имеет вид

,

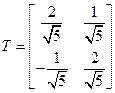формулы преобразования осей координат имеют вид

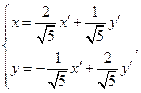(1)

Подставив в уравнение данной кривой выражения для x и y из (1), имеем

После несложных преобразований получим

.

Применив метод выделения полного квадрата, получим:

С помощью формул параллельного переноса системы координат

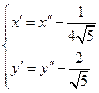
получаем

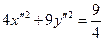или .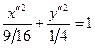

Это уравнение эллипс с полуосями .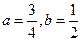

Задача 3. Найти неопределённые интегралы. В пунктах a и b результаты интегрирования проверить дифференцированием.

Решение.

3.a.

Преобразуем подынтегральную функцию таким образом, чтобы в числителе получилась производная знаменателя:

Проверим полученный результат:

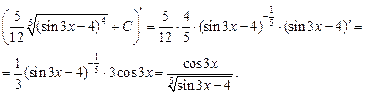
3.b.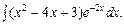

Воспользуемся методом интегрирования по частям, основанном на следующей формуле: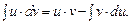

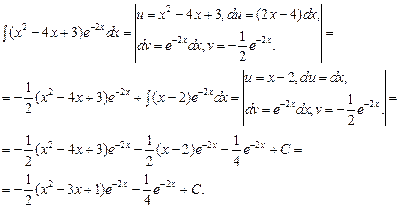
Выполним проверку результата:

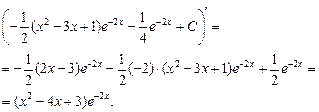
3.c.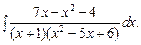

Подынтегральная функция представляет собой рациональную дробь. Разложим её знаменатель на множители: 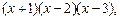тогда:

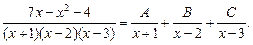
Приведя правую часть последнего равенства к общему знаменателю, и приравняв числители дробей, получим тождество:

Найдём искомые коэффициенты:

а) полагая , получаем 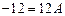, откуда ;

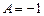б) полагая 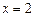, получаем 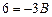, откуда ;

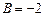в) полагая 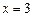, получаем 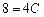, откуда ;

Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

3.d.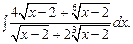

Подынтегральная функция представляет собой интеграл вида:

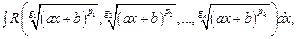
Где 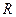- рациональная функция; 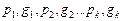- целые положительные числа. С помощью подстановки 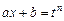(здесь 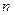- наименьшее общее кратное (НОК) знаменателей 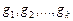) данный интеграл приводится к интегралу от рациональной функции.

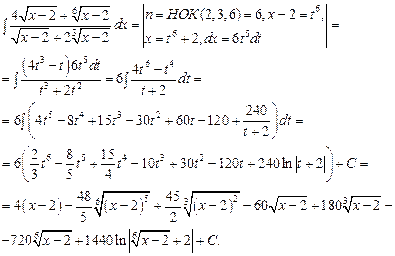
Задача 4. Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением третьего десятичного знака.

Решение. Формула Симпсона или формула парабол имеет вид:

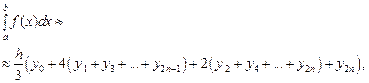(1)

где .

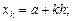
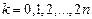Рассмотрим при 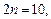тогда .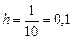

Составим таблицу значений подынтегральной функции, необходимых для вычисления данного интеграла.

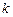
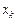
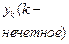
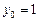
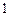
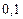
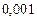
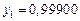
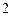
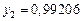
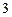
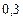
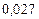
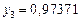
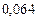
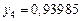
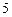
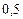
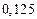
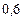
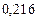
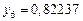
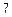
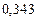
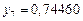
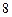
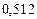
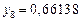
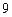
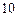
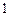
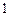
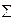
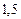
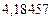
В последней строке таблицы находятся суммы чисел соответствующих столбцов.

Так как

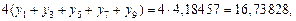
по формуле (1) находим

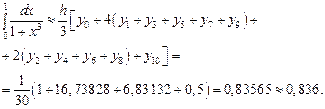
Задача 5. Вычислить несобственные интегралы или доказать их расходимость.

Решение. В соответствииопределениемнесобственных интегралов имеем

5.a.

5.b.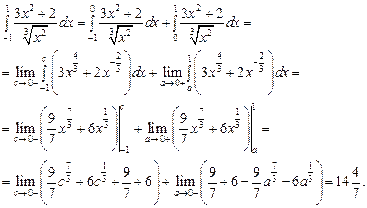

Задача 6.

6.a. Вычислить площадь фигуры, ограниченной линиями

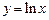и .

Решение. Построим графики данных кривых:

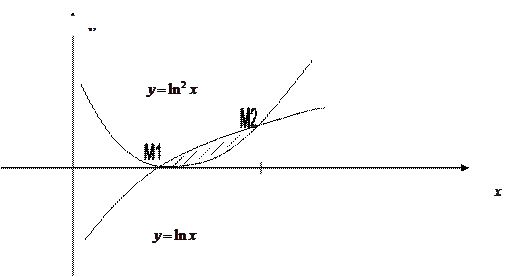
Найдём точки пересечения данных кривых: 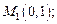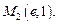Тогда по формуле 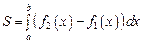имеем:

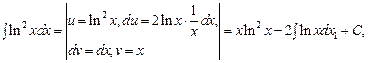
Окончательно имеем:

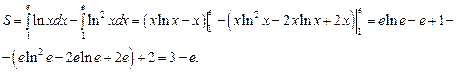
6.b. Найти координаты центра масс однородной фигуры, ограниченной кривыми и .

Решение. Построим графики данных кривых:

Для отыскания 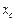и воспользуемся формулами:

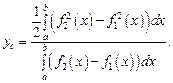
Найдём точки пересечения кривых: и 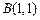, тогда ,

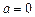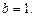
Имеем:

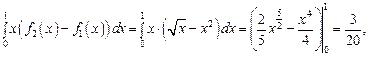
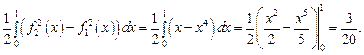
Откуда

Задача 7. Найти область определения функции .

Решение. Логарифмическая функция определяется только при положительном значении аргумента, поэтому 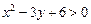, или .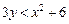

Значит, границей области будет линия , т.е. парабола.

Из неравенства получаем, что областью определения данной функции является заштрихованная часть плоскости без точек параболы.

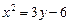
Задача 8. Найти частные производные 1-го порядка функции .

Решение. Находим частную производную по x данной функции, считая y постоянной и используя формулу дифференцирования сложной функции одной переменной:

,

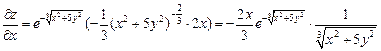аналогично вычисляем производную по y.

.

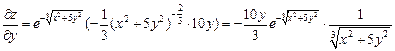Задача 9. Даны функция 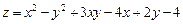, точка А(-1;0), вектор .

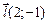Найти:

9.а. grad z в точке А;

9.b. производную функции f(x,y) в точке А в направлении ;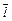

9.c. уравнение касательной плоскости и нормали к поверхности z=f(x,y) в точке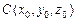

Решение.

9.а. По определению grad z= .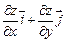

Вычислим частные производные и их значения в точке А.

; ; ; .

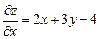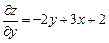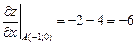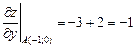Следовательно: grad .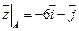

9.b. Справедлива формула (1) , где 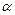- угол, образованный вектором 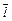с осью OX.

Здесь ; .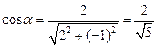

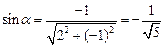Тогда, применяя формулу (1), получим:

.

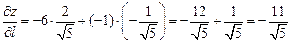9.c. Найдём значение функции 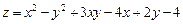в точке А(-1;0). 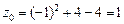. Тогда С(-1;0;1).

Уравнение касательной плоскости к поверхности z=f(x,y) в точке 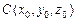имеет вид

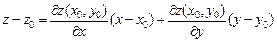, (2)

а уравнение нормали –

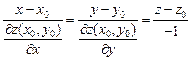. (3)

Подставим найденные значения частных производных в точке А(-1;0) в формулу (2), найдём уравнение касательной плоскости в точке С(-1;0;1): 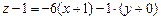или 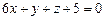, а уравнение нормали на основании формулы (3) запишется в виде: .

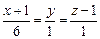Задача 10. Найти экстремум функции .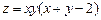

Решение. Находим стационарные точки функции. Для этого вычисляем первые частные производные данной функции:

; .

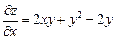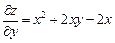Приравнивая их к нулю, получаем систему уравнений

,

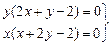из которой определяем стационарные точки данной функции:

, , , .

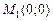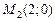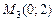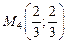Теперь воспользуемся достаточными условиями экстремума. Вычислим вторые частные производные:

, , ,

.

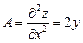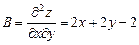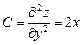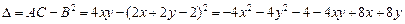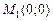
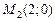
Имеем: для точки , т.е. экстремума нет, для точки 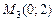, т.е. экстремума нет, для точки , т.е. экстремума нет, для точки 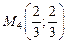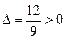, , 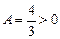т.е. имеем точку локального минимума функции, в которой .

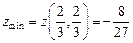Задача 11. Найти наибольшее и наименьшее значение функции 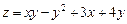в области 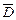, ограниченной линиями x=0, y=0, x+y-1=0.

Решение. Область задания функции представляет собой треугольник, ограниченный координатными осями и прямой x+y =1.

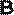Выясним, существуют ли стационарные точки, лежащие внутри данной области 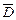, т.е. внутри треугольника ОАВ.

Имеем

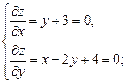х=-10, у=-3

Получили точку М(-10; 3). Она не принадлежит области 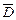, следовательно значение функции в ней не учитываем.

Исследуем значения функции на границе области 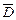. Поскольку граница состоит из трёх участков, описанных тремя разными уравнениями, то приходится исследовать функцию на каждом участке отдельно.

Исследуем функцию на участке ОА, где А(1;0). Уравнением связи является у=0. С учётом его функция представима в виде z=3х. Так как 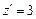, то стационарных точек на отрезке ОА нет. Найдём значение функции z=3x в точке О и А соответственно , .

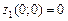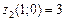Исследуем функцию на участке ОВ, где В(0;1). Уравнением связи является у=0. С учётом его функция представима в виде 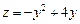. Тогда . Находим стационарную точку из уравнения 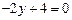; получаем, что у=2. Стационарная точка 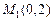не принадлежит области 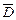. Значение функции в точке В .

Исследуем функцию вдоль участка прямой х+у=1. Подставляя у=1-х в выражение для функции, получим: 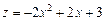, тогда 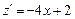, -4х+2=0, 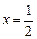, 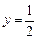. Стационарная точка 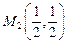принадлежит области 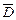. Значение функции в ней .

Сравниваем значения 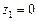, , 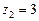, , заключаем, что 3,5 – наибольшее значение функции, достижимое в точке 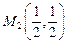, а 0 – наименьшее значение, достигаемое в точке (0,0).

, .

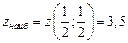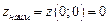Задача 12. Вычислить повторный интеграл

.

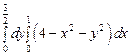Решение. Чтобы вычислить повторный интеграл, нужно вычислить внутренний, а потом – внешний [1, с. 382], при этом при вычислении внутреннего интеграла переменная интегрирования внешнего интеграла (в данном случае переменная 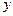) считается постоянной. Следовательно,

=

.

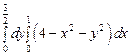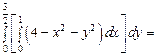
Задача 13. Изменить порядок интегрирования в следующих интегралах:

13.a. ;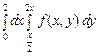

13.b. .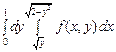

Решение. Для решения следует изучить [1, с. 382-384].

13.a. Изобразим область интегрирования на чертеже (рис. 1): она ограничена линиями , , , .

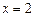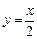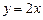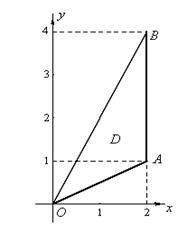
Рис. 1

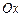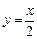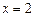Эта область является правильной и в направлении оси , однако ее правая граница задается двумя линиями: отрезками прямых и , поэтому ее придется разбить на две части. Следовательно

.

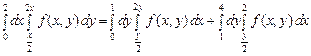13.b. Область интегрирования ограничена линиями 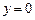, , , 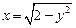(рис. 2).

Рис. 2

Она является правильной и в направлении оси 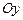, но ее верхняя граница состоит из двух линий: дуги параболы и дуги окружности . Следовательно, ее придется разбить на две части, поэтому

.

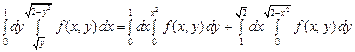Задача 14. Вычислить криволинейный интеграл

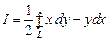
по контуру треугольника 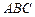, где , , .

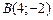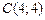Решение. Так как контур треугольника состоит из трех отрезков (сторон треугольника), то

,

при этом мы предполагаем, что контур 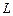обходится против часовой стрелки.

Рассмотрим отдельно каждый интеграл.

Уравнение 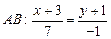, , 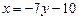тогда 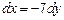, , 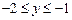т.е. считаем, что 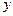– параметр. Следовательно

.

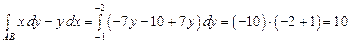Уравнение 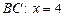, тогда 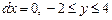, поэтому

.

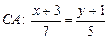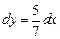Уравнение , , тогда , , поэтому

.

Отв.: .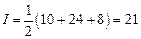

Задача 15. Вычислить криволинейный интеграл

,

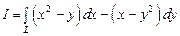пробегая против часовой стрелки верхнюю дугу окружности .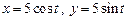

Решение. Если точка пробегает верхнюю дугу окружности против часовой стрелки, то параметр 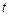изменяется от 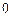до 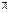: 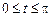. Так как , , то

.

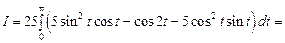
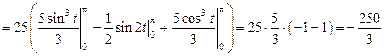Отв.: .

Не нашли, что искали? Воспользуйтесь поиском: