Задачи для контрольной работы. 3 страница

Задача 4.

В задаче нужно вычислить интеграл с помощью формулы Симпсона при указанных значениях параметра, разбив интервал интегрирования на 10 частей. Все вычисления производить с округлением до 3-его десятичного знака числа. Параметр p равен последней цифре номера варианта плюс 1.

4.1 – 4.10

4.11 – 4.20

4.21 – 4.30

4.31 – 4.40

4.41 – 4.50

4.51 – 4.60

4.61 – 4.70

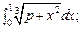
4.71 – 4.80

4.81 – 4.90

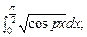
4.91 – 4.100

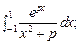
Задача 5

Вычислить несобственные интегралы или доказать их расходимость:

5.1.

5.2.

5.3.

5.4.

5.5.

5.6.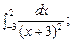

5.7.

5.8.

5.9.

5.10.

5.11.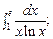

5.12.

5.13.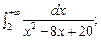

5.14.

5.15.

5.16.

5.17.

5.18.

5.19.

5.20.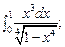

5.21.

5.22.

5.23.

5.24.

5.25.

5.26.

5.27.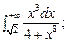

5.28.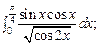

5.29.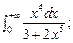

5.30.

5.31.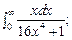

5.32.

5.33.

5.34.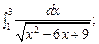

5.35.

5.36.

5.37.

5.38.

5.39.

5.40.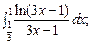

5.41.

5.42.

5.43.

5.44.

5.45.

5.46.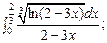

5.47.

5.48.

5.49.

5.50.

5.51.

5.52.

5.53.

5.54.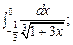

5.55.

5.56.

5.57.

5.58.

5.59.

5.60.

5.61.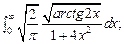

5.62.

5.63.

5.64.

5.65.

5.66.

5.67.

5.68.

5.69.

5.70.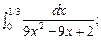

5.71.

5.72.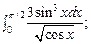

5.73.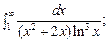

5.74.

5.75.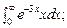

5.76.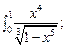

5.77.

5.78.

5.79.

5.80.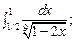

5.81.

5.82.

5.83.

5.84.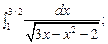

5.85.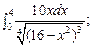

5.86.

5.87.

5.88.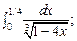

5.89.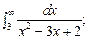

5.90.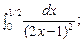

5.91.

5.92.

5.93.

5.94.

5.95.

5.96.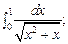

5.97.

5.98.

5.99.

5.100.

Задача 6

6.1. Вычислить площадь фигуры, ограниченной параболой и прямой .

6.2. Вычислить площадь фигуры, ограниченной одной аркой циклоиды 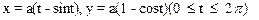и осью Ох.

6.3. Вычислить площадь фигуры, ограниченной кардиоидой .

6.4. Вычислить площадь фигуры, ограниченной двухлепестковой розой .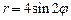

6.5. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами и .

6.6. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом , параболой и осью Оу.

6.7. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми и .

6.8. Вычислить длину дуги полукубической параболы от точки A(2;0) до точки B (6;8)

6.9. Вычислить длину кардиоиды .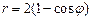

6.10. Вычислить длину одной арки циклоиды .

6.11. Вычислить площадь фигуры, ограниченной параболами и .

6.12. Вычислить площадь фигуры, ограниченной параболой и локоном Аньези .

6.13. Вычислить площадь фигуры, ограниченной кривой .

6.14. Вычислить площадь фигуры, ограниченной четырехлепестковой розой .

6.15. Вычислить площадь фигуры, ограниченной эллипсом .

6.16. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной эллипсом .

6.17. Вычислить длину кривой между точками пересечения с осями координат.

6.18. Вычислить длину полукубической параболы от точки O(0; 0) до точки M .

6.19. Найти длину дуги полукубической параболы , заключенной внутри окружности .

6.20. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой 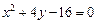и осью Ох.

6.21. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболам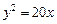и и .

6.22. Найти координаты центра тяжести однородной дуги астроиды , расположенной над осью Оx.

6.23. Найти координаты центра тяжести однородной дуги одной арки циклоиды .

6.24. Найти координаты центра тяжести фигуры, ограниченной эллипсом и осями координат Ох и Оу .

6.25. Найти работу, совершаемую при выкачивании воды из корыта, имеющего форму полуцилиндра, длина которого а = 2м, радиус r = 0.3м.

6.26. Найти силу давления бензина, находящегося в цилиндрическом баке высотой h = 3м и радиусом основания r = 1 м, на его стенки. Плотность бензина р.

6.27. В жидкость с плотностью р погружена круглая пластинка диаметром d = 1.5м, касающаяся поверхности жидкости. Найти силу давления жидкости на пластинку.

6.28. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги кривой от до .

6.29. Найти длину дуги кривой .

6.30. Найти площадь фигуры, ограниченной линиями .

6.31. Вычислить площадь фигуры, ограниченной параболой и прямой .

6.32. Вычислить площадь фигуры, ограниченной гиперболой и прямой .

6.33. Вычислить площадь фигуры, ограниченной кардиоидой 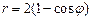и окружностью r = 4.

6.34. Вычислить площадь фигуры, ограниченной одной аркой циклоиды и осью Ох.

6.35. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной цепной линией , осью Ох и прямыми х = ±1.

6.36. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболами у = х² .

6.37. Вычислить объем тела, образованного вращени­ем вокруг оси Оу фигуры, ограниченной локоном Аньези , прямой 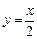и осью Оу.

6.38. Вычислить длину дуги полукубической параболы 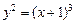от x = 0 до x = 3.

6.39. Вычислить длину астроиды .

6.40. Вычислить длину кардиоиды .

6.41. Найти координаты центра тяжести однородной дуги цепной линии от точки (0, 1) до точки .

6.42. Найти координаты центра тяжести дуги астроиды , расположенной в первом квадранте, если линейная плотность в каждой ее точке равна абсциссе точки.

6.43. Деревянная прямоугольная балка, размеры поперечного сечения которой а = 0,4 м, b = 0,2 м, длина l = 4,5 м, плавает на поверхности воды. Удельный вес дерева у = 0,8 Г/см³. Вычислить работу, необходимую для извлечения балки из воды.

6.44. Растяжение (удлинение) пружины пропорционально приложенной силе. Вычислить работу, затрачиваемую при растяжении пружины на 6 см, если сила, равная 2 кГ, удлиняет ее на 1 см.

6.45. Вычислить работу, которую необходимо затратить, чтобы выкачать воду из сосуда, имеющего форму прямого круглого конуса с вертикальной осью, обращенного вершиной вниз, если радиус основания конуса r = 2 м и высота h = 5 м.

6.46. Вертикальная плотина имеет форму параболического сегмента, высота которого h— 12 м, а верхнее осно­вание совпадает с уровнем воды и имеет длину а = 30 м. Вычислить силу давления воды на плотину.

6.47. Вертикальная плотина имеет форму равнобочной трапеции, верхнее основание которой совпадает с уровнем воды и имеет длину а = 50 м, нижнее основание b = 20 м, а высота h = 15 м. Вычислить силу давления воды на плотину.

6.48. Найти координаты центра тяжести однородной плоской фигуры, ограниченной дугой косинусоиды и отрезком оси Ох от х = 0 до .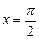

6.49. Найти координаты центра тяжести однородной плоской фигуры, ограниченной дугой синусоиды и отрезком оси Ох от х = 0 до .

6.50. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболами .

Вычислить работу, которую необходимо затратить на выкачивание воды из резервуара Р. Удельный вес воды при­нять равным 9,81кН/м, = 3,14. (Результат округлить до целого числа.)

6.51. Р: правильная четырехугольная пирамида со сторо­ной основания 2м и высотой 5м.

6.52. Р: правильная четырехугольная пирамида, обращенная вершиной вниз. Сторона основания пирамиды равна 2 м, высота — 6м.

6.53. Р: котел, имеющий форму сферического сегмента, высота которого 1,5м и радиус 1м.

6.54. Р: полуцилиндр, радиус основания которого 1 м, дли­ на 5м.

6.55. Р: усеченный конус, у которого радиус верхнего основания равен 1м, нижнего — 2м, высота — Зм.

6.56. Р: желоб, перпендикулярное сечение которого явля­ется параболой. Длина желоба 5 м, ширина 4 м, глубина 4 м.

6.57. Р: цилиндрическая цистерна, радиус основания ко­ торой 1м, длина 5м.

6.58. Р: правильная треугольная пирамида с основанием 2м и высотой 5м.

6.59. Р: правильная треугольная пирамида, обращенная вершиной вниз, сторона основания которой 4 м, высота 6 м.

6.60. Р: конус, обращенный вершиной вниз, радиус основания которого 3 м, высота 5м.

6.61. Р: усеченный конус, у которого радиус верхнего основания равен 3 м, нижнего — 1м, высота — 3м.

6.62. Р: конус с радиусом основания 2 м и высотой 5 м.

6.63. Р: правильная четырехугольная усеченная пирамида, у которой сторона верхнего основания 8 м, нижнего — 4 м, высота— 2м.

6.64. Р: параболоид вращения, радиус основания которо­го 2м, глубина 4м.

6.65. Р: половина эллипсоида вращения, радиус основания которого 1м, глубина 2м.

6.66. Р: усеченная четырехугольная пирамида, у которой сторона верхнего основания равна 2 м, нижнего — 4 м, высо­та — 1м.

6.67. Р: правильная шестиугольная пирамида со стороной основания 1 м и высотой 2м.

6.68. Р: правильная шестиугольная пирамида с верши­ной, обращенной вниз, сторона основания которой 2 м, высота 6м.

6.69. Р: цилиндр с радиусом основания 1 м и высотой 3 м.

6.70. Р: правильная усеченная шестиугольная пирамида, у которой сторона верхнего основания равна 1 м, нижнего — 2 м, высота — 2 м.

6.71. Р: желоб, в перпендикулярном сечении которого лежит полуокружность радиусом 1м, длина желоба 10 м.

6.72. Р: правильная усеченная шестиугольная пирамида, у которой сторона верхнего основания равна 2 м, нижнего — 1м, высота — 2м.

6.73. Р: полусфера радиусом 2м.

Вычислить работу, затрачиваемую на преодоление силы тяжести при построении сооружения Q из некоторого матери­ала, удельный вес которого - (Результат округлить до целого числа.)

6.74. Q: правильная усеченная четырехугольная пирами­ да, сторона верхнего основания которой равна 2 м, нижнего 4м, высота 2м; = 24кН/м³.

6.75. Q: правильная шестиугольная пирамида со сторо­ной основания 1м и высотой 2м; — 24кН/ м³.

6.76. Q: правильная четырехугольная пирамида со стороной основания 2м и высотой 4м; - 24кН/ м³.

6.77. Q: правильная шестиугольная усеченная пирамида, сторона верхнего основания которой равна 1 м, нижнего 2м, высота — 2м; = 24кН/м³.

6.78. Q: правильная треугольная пирамида со стороной основания 3 м и высотой 6м; = 20кН/м³.

6.79. Q: конус, радиус основания которого 2 м, высота 3 м; = 20 кН/м³.

6.80. Q: усеченный конус, радиус верхнего основания которого равен 1 м, нижнего — 2 м, высота — 2 м; — 21 кН/ м³

Найти координаты центра масс плоской однородной фигуры Ф, ограниченной данными линиями.

6.81. Ф — треугольник, стороны которого лежат на пря­мых х + у = a, x = 0 и y = 0.

6.82. Ф ограничена эллипсом х²/а² + у²/b² = 1 и осями координат (х 0, у 0).

6.83. Ф ограничена первой аркой циклоиды

х — a(t — sin t), у = a(l — cost) и осью Ох.

6.84. Ф, ограничена кривыми у = х², .

6.85. Ф ограничена дугой синусоиды у = sin x и отрезком оси Ох ().

6.86. Ф ограничена полуокружностью и осью Ох.

6.87. Ф ограничена дугой параболы (а > 0, b > 0), осью Ох и прямой х = b.

6.88. Ф ограничена дугой параболы (а > 0, b > 0), осью Оy и прямой y = b.

6.89. Ф ограничена замкнутой линией у² = ах³ - х⁴.

6.90. Ф ограничена осями координат и дугой астроиды, расположенной в первом квадранте.

6.91. Ф — сектор круга радиусом R с центральным углом,равным 2а.

6.92. Ф ограничена кардиоидой = а(1 +cos ).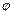

6.93. Ф ограничена первой петлей лемнискаты Бернулли = a²cos2 .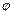

6.94. Ф ограничена осями координат и параболой .

6.95. Фограничена полукубической параболой ау² = х³ и прямой х = а (а > 0).

6.96.

6.97.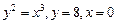

6.98.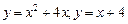

6.99. r = 3 + sin2 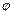между смежными наибольшим и наименьшим радиус-векторами.

6.100. r = 2 — cos3 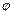между смежными наибольшим и наименьшим радиус-векторами.

Задача 7. Определить и изобразить область существования следующей функции:

7.1. ; 7.2. ;

Не нашли, что искали? Воспользуйтесь поиском: