Контрольные работы.

Программой дисциплины «Математика» для студентов I курса предусмотрено выполнение контрольных работ №1, №2.

3.1. При выполнении контрольной работы №1 необходимо изучить элементы линейной и векторной алгебры, аналитической геометрии на плоскости и в пространстве, а также ознакомиться с теорией пределов. Научиться вычислять основные типы пределов - неопределенности , первый и второй замечательный пределы. Изучить понятие непрерывности функции, точки разрыва и их классификация.

Задание 1. Найти решение системы с помощью правила Крамера.

Для систем трех уравнений с тремя неизвестными

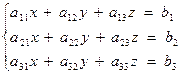
правило Крамера имеет вид: ,

где

Определитель третьего порядка, обозначаемый символом

∆=

и вычисляется по правилу треугольника:

.

Например (см. Задание №1 контрольной работы №1).

Решение.

.

Ответ: (1, -2, 3).

Задание №2. По координатам вершины пирамиды А₁А₂А₃А₄ найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) площадь грани А₁А₂А₃;

4) объем пирамиды;

5) уравнения плоскостей А₁А₂А₃ и А₁А₂А₄ ;

6) угол между плоскостями А₁А₂А₃ и А₁А₂А₄.

1) Если заданы точки A₁(x₁, y₁, z₁), А₂(x₂, y₂, z₂), то координаты вектора:

тогда длина вектора вычисляется по формуле .

2) Из определения скалярного произведения следует, что угол между векторами вычисляется по формуле:

.

3) - площадь треугольника, построенного на векторах и .

4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу вычисления объема пирамиды: .

5) Если даны три точки А₁(x₁; y₁; z₁), А₂(x₂; y₂; z₂) и А₃(x₃; y₃; z₃), то уравнение плоскости, проходящей через три точки находится по формуле:

(1)

Например(см. Задание №2 контрольной работы №1).

Составитьуравнение плоскости, проходящей через три точки А₁ , А₂ ,А₃, если А₁(-3, 2, 0), А₂(-2, 0, 2), А₃(0, 3, -1).

Решение: по формуле (1) получим ,

Итак, уравнение плоскости имеет вид −4х+7у+7z-26=0, где нормаль имеет координаты N(-4; 7; 7).

6) Угол, образованный двумя плоскостями, находится по формуле

где - нормали плоскостей.

Задание №3. Даны вершины треугольника АВС, найти:

1) уравнение сторон ∆АВС;

2) уравнение высоты, проведенной из вершины А;

3) длину высоты.

1) Уравнение прямой, проходящей через две точки имеет вид

.

2) Для нахождения уравнения высоты используют условие перпендикулярности прямых и уравнение прямой проходящей через данную точку с угловым коэффициентом k: у-у₀=k(x-x₀).

Задание №4. Вычислить пределы функций, не пользуясь правилом Лопиталя.

При вычислении предела дробно-рациональной функции при 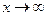числитель и знаменатель дроби—величины бесконечно большие, т.е. получаем выражение которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень х.

Пример 1 (см. Задание №4(а) контрольной работы №1).

Решение. Для вычисления предела этой функции нужно числитель и знаменатель разделить на :

(при 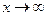слагаемые — величины бесконечно малые и, следовательно, их пределы равны нулю).

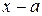В том случае, когда при вычислении предела дробно-рациональной функции при числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность , надо разделить их на и перейти к пределу. Если после деления окажется, что при числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на .

Пример 2 (см. Задание №4(б) контрольной работы №1).

.

Решение. Пределы числителя и знаменателя при равны нулю, т.е.:

Разложим квадратный трёхчлен в числителе на линейные множители по формуле где и — корни трёхчлена. Разложив на множители и знаменатель, сократим дробь на , получим:

.

При вычислении пределов тригонометрических функций часто используется первый замечательный предел и его следствия:

Пример 3 (см. Задание №4(в) контрольной работы №1).

Решение. Преобразовав разность косинусов в произведение, получим

Если в пределе получаем неопределенность , используем второй замечательный предел (2)

Пример 4 (см. Задание №4(г) для вариантов 4,5,7,8 контрольной

работы №1).

Решение. Выполнив преобразования и применив второй замечательный предел, найдём

Пример 5 (см. Задание №4(г) для вариантов 1-3,6,9,10 контрольной

работы №1).

Решение. Выполнив преобразования и применив формулу (2), найдём

Задание №5. Исследовать функцию на непрерывность: найти точки разрыва функции и определить их тип.

Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

.

Это равенство означает выполнение трех условий:

1) функция f(x) определена в точке х₀ и ее окрестности;

2) функция f(x) имеет предел при х→х₀;

3) предел функции в точке х₀ равен значению функции в этой точке

Если в точке х=х₀ не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва.

Все точки разрыва разделяются на точки разрыва первого и второго рода.

Точка разрыва х₀ называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. и .

При этом: 1) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва;

2) если А_1≠ А₂ , то х₀ называется точкой конечного разрыва, а величину / А₁ - А₂ / называют скачком функции.

Точка разрыва х₀ называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

Например (см. Задание №5 контрольной работы №1).

Дана функция . Найти точки разрыва, определить их тип.

Решение:

Функция f(x) определена и непрерывна на всей числовой оси, кроме точки х=3.

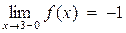Очевидно, что , следовательно , . Поэтому в точке х=3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1-(-1)=2.

3.2. При выполнении контрольной работы №2 необходимо изучить основы дифференциального исчисления функции одной и нескольких переменных, а также их приложения к вычислению пределов, исследованию функции одной и нескольких переменных.

Задание №1. Найти производные первого порядка данных функций.

При выполнении данного задания необходимо знать правила вычисления производной (производная суммы, произведения и частного дух функций), а также изучить таблицу производных.

Например (см. Задание №1 контрольной работы №2).

1) у = соsx×ln²x.

y^/ = (cosx)^/ ln²x + cosx (ln²x)^/ = - sinx ln²x + cosx×2lnx×(lnx)^/ =

=- sinx×ln²x +cosx×2lnx×().

2) y =

y^/ = .

 

3) Найти у^/.

Производная функции, заданной параметрически вычисляется по формуле: .

x^/_t = 2 а sint×cost; y^/_t = -3 а cos²t×sint, тогда у^/ = = -1,5cost.

 

Задание №2. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить график.

Общая схема исследования функции и построения графика.

1. Найти область определения функции.

2. Определить тип функции (четность, нечетность).

3. Найти точки пересечения с осями координат и интервалы

знакопостоянства функции.

4. Найти асимптоты графика функции:

а) вертикальные; б) невертикальные (наклонные).

5. Найти точки возможного экстремума и интервалы возрастания и

убывания функции.

6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.

7. Построить график функции, учитывая проведенные исследования.

Например (см. Задание №2 контрольной работы №2).

Построить график функции .

1. Областью определения функции является множество всех действительных

чисел, кроме х=1 (в этом случае знаменатель равен нулю).

2. Для определения типа функции найдем значение

следовательно функция

 

не является ни четной ни нечетной (общего вида).

3. Так как уравнение х²+1=0 не имеет действительных корней то график

функции не имеет точек пересечения с осью Ох, но пересекает ось Оу в

точке (0;-1).

Определим интервалы знакопостоянства функции:

_ +

|

y(x)ниже оси Ох выше оси Ох х

4. Найдем асимптоты графика функции.

а). Исследуем поведение функции вблизи точки разрыва х=1:

 

 

 

Следовательно прямая х=1 является вертикальной асимптотой.

б). Определим существование наклонной асимптоты:

 

 

Из этого вытекает, что график функции имеет наклонную асимптоту у=х+1.

5. Для нахождения точек возможного экстремума найдем производную функции:

 

 

y'(x)=0 в точках

 

Исследуем знак производной: y' +   +

х

у 1

Получаем, что функция

возрастает на промежутках:

убывает на промежутках:

Точки экстремума:

 

6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:

 

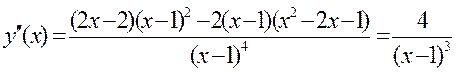Так как у’’(х) в нуль не обращается, то критических точек нет.

Исследуем знак второй производной:

 

у"   + +

1 х

Следовательно

на интервале (-∞; 1) график направлен выпуклостью вверх (выпуклый), а на интервале (1; +∞) – выпуклостью вниз (вогнутый).

 

у

 

 

х

 

Задание № 3.

Найти grad z в точке М₀. Вычислить длину полученного вектора.

Градиентом функции z=f(x,y) в точке M(x,y) называется вектор с началом в точке М, имеющий своими координатами частные производные функции z: grad z = (, ).

Длина вектора вычисляется по формуле рассмотренной в К.р.№1 задание 2.

Например (см. Задание №3 контрольной работы №2).

Найти градиент функции z = e^3x+2y в точке М(0,1).

Решение:

= 3e^3x+2y, = 2e^3x+2y;

= 3e², = 2e², следовательно, grad z(М) = (3e², 2e²).

Задание №4.

Найти экстремумы функции двух переменных (в сомнительном случае дополнительно исследовать необязательно)

Алгоритм нахождения экстремума функции двух переменных:

1. Найти z^/_x и z^/_y.

2. Решить систему уравнений причем каждое решение этой системы будет стационарной точкой.

3. Найти z^//_xх, z^//_xy и z^//_yу. Вычислить А, В, С, D.

4. Применить теорему о достаточном условии экстремума.

5. Если стационарная точка окажется точкой экстремума, то вычислить z_max (z_min).

Теорема (достаточное условие экстремума).

Пусть в некоторой стационарной точке М₀(х₀,у₀) и некоторой ее окрестности функция z=f(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим:

А = , В = , С =

И составим дискриминант D = АС – В². Тогда

1) если D > 0, то функция имеет в точке М₀ экстремум, а именно

максимум при А<0 (или С<0),

минимум при А>0 (или С>0);

2) если D > 0, то в точке М₀ экстремума нет;

3) если D = 0, то требуются дополнительные исследования (сомнительный случай).

Например (см. Задание №4 контрольной работы №2).

Найти экстремум функции z = x³ + у³ – 3хy.

Решение:

1. Находим частные производные первого порядка от функции z:

z^/_x = 3х² – 3у и z^/_y = 3у² – 3х.

2. Значит получаем систему уравнений , решая которую получаем

две стационарные точки М₁(0,0) и М₂(1,1).

3. Находим частные производные 2-го порядка z^//_xх = 6х, z^//_xy = -3 и z^//_yу = 6у.

4а) М₁(0,0): А =0, В = -3, С = 0 Þ D = -9 < 0, значит по теореме получаем,

что в т. М₁(0,0) экстремума нет.

4б) М₂(1,1): А=6, В = -3, С = 6 Þ D = 27 > 0, значит по теореме, получаем, что

т. М₂(1,1) является точкой минимума (т.к. А>0).

5. Вычислим теперь z_min = z (1,1) = - 1.

Ответ: z_min = -1.

Не нашли, что искали? Воспользуйтесь поиском: