Метод математической индукции

Вопрос

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:

· P(1) является истинным предложением (утверждением);

· P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).

Таким образом, метод математической индукции предполагает два этапа:

· Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).

· Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).

Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:

Пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m.

Если:

· P(m) справедливо;

· P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.

Вопрос

2.Метод логического следования

Отношение между высказываниями; более точно — отношение между посылками и заключением, которое характеризуется тем, что заключение с необходимостью следует из посылок.
Пример: Логическое завершения чего либо, «Я повернул ключ, и дверь открылась»

Вопрос

Доказательство от противного.
Доказательство от противного (лат. reductio ad absurdum), вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение противоречащего ему суждения - антитезиса. Опровержение антитезиса при этом достигается установлением факта его несовместимости с каким-либо заведомо истинным суждением. Этой форме Д. от п. соответствует следующая схема доказательства: если В истинно и из А следует ложность В, то А - ложно. Другая, более общая форма Д. от п. - это доказательство путём опровержения (обоснования ложности) антитезиса по правилу: допустив А, мы вывели противоречие, следовательно - не-А. Здесь А может быть как утвердительным, так и отрицательным суждением, а вывод противоречия может пониматься либо как вывод утверждения о тождестве заведомо различных предметов, либо как вывод пары суждений В, не-В, либо как вывод конъюнкции этой пары, либо как вывод эквивалентности этой пары. Этим различным случаям соответствуют различные интерпретации понятий Д. от п. и «противоречие». Приём Д. от п. особенно важен в математике: многие отрицательные суждения математики не могут быть доказаны другим путём, кроме приведения к противоречию

Вопрос

Метод факторизации Ферма — алгоритм факторизации (разложения на множители) нечётного целого числа 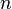, предложенный Пьером Ферма (1601-1665) в 1643 году.

Метод основан на поиске таких целых чисел и 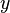, которые удовлетворяют соотношению , что ведёт к разложению .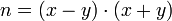

Метод Ферма основан на теореме о представлении числа в виде разности двух квадратов:

Если нечетно, то существует взаимно однозначное соответствие между разложениями на множители и представлениями в виде разности квадратов с , задаваемое формулами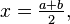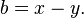

Доказательство^[4]

Если задана факторизация , то имеет место соотношение: . Таким образом получается представление в виде разности двух квадратов.

Обратно, если дано, что , то правую часть можно разложить на множители: .

Описание алгоритма

Для разложения на множители нечётного числа 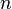ищется пара чисел таких, что , или . При этом числа и являются множителями 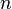, возможно, тривиальными (то есть одно из них равно 1, а другое — .)

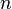Равенство равносильно 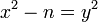, то есть тому, что является квадратом.

Поиск квадрата такого вида начинается с — наименьшего числа, при котором разность неотрицательна. Для каждого значения начиная с , вычисляют и проверяют, не является ли это число точным квадратом. Если не является — то увеличивают на единицу и переходят на следующую итерацию.

Если является точным квадратом, т.е. то получено разложение:

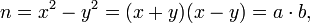в котором

Если оно является тривиальным и единственным, то 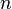— простое.

На практике значение выражения на -ом шаге вычисляется с учетом значения на -ом шаге:

где

Примеры

Не нашли, что искали? Воспользуйтесь поиском: