Равносильности, выражающие одни логические операции через другие.

1. 4. .

2. . 5. .

3. . 6. .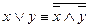

Здесь 3, 4, 5, 6 – законы Моргана.

Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4, соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.

Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем одну из них: первую.

Так как при одинаковых логических значениях x и y истинными являются формулы , то истинной будет и конъюнкция . Следовательно, в этом случае обе части равносильности имеют одинаковые истинные значения.

Пусть теперь x и y имеют различные логические значения. Тогда будут ложными эквивалентность и одна из двух импликаци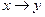й или . Но при этом будет ложной и конъюнкция .

Таким образом, и в этом случае обе части равносильности имеют одинаковые логические значения.

Аналогично доказываются равносильности 2 и 4.

Из равносительностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.

Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание не может быть выражена с помощью операции конъюнкции.

Однако существуют операции, с помощью которых может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция “Штрих Шеффера”. Эта операция обозначается символом ½ и определяется следующей таблицей истинности:

Не нашли, что искали? Воспользуйтесь поиском: