
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Предикаты. Навешивание кванторов.Страницы 72-74



Вопрос
Вопрос
ЛИНЕЙНАЯ МОДЕЛЬ— модель, отображающая состояние или функционирование системы таким образом, что все взаимозависимости в ней принимаются линейными. Соответственно она может формулироваться в виде одного линейного уравнения или системы линейных уравнений. Причем в ряде случаев нелинейность взаимозависимостей может приводиться к линейной форме путем математических преобразований переменных: например, в нелинейных соотношениях.
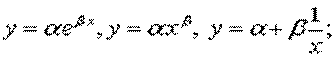
в первом и втором случаях логарифмирование обеих частей уравнений обеспечивает связь линейную в логарифмах lny = lnα + βx; lny = lnα + βlnx, а в третьем — линейно зависимы y и 1/x.
yi = αi + βx + ui.
В этой регрессионной линейной модели приняты следующие обозначения: свободный член α и вектор β — параметры; u — случайная ошибка, математическое ожидание которой равно нулю; x — вектор переменных xi, идентифицированных как оказывающие воздействие на переменную y (т. е. управляющих переменных). Применяется также иная система обозначений: переменная величина X называется объясняющей (независимой) переменной; переменная Y — объясняемой (зависимой) переменной; u — остаток, равный разнице между между фактическими значениями и значениями модели. (См. Регрессионный анализ.) Л. м. в виде системы уравнений в общей форме записывается:
yi = αi + Bxi + ui,
где yi — зависимая переменная; B ≡ [βij] — матрица параметров модели; xi — вектор управляющих переменных в i-м уравнении.
Вопрос
Вопрос
Квадратичная модель
Итак, линейная модель является только приближением, в случае если в портфель входят опционы. Однако мы вычисляли и вторую производную по цене, которую называли гамма.
Поэтому можно построить и квадратичную модель изменения цены портфеля.
(P= (S * (+ 0.5(((S)^2
Опять, полагая
(x = (S / S,
получим
(P= S * (*(x + 0.5S^2(((x)^2
Однако в этом случае величина (P уже не будет иметь нормальное распределение.
Пусть (x имеет нормальное распределение со средним 0 и стандартным отклонением (
Тогда первые три момента для (P будут
E((P) = 0.5S^2((^2
E((P)^2 = S^2 (^2(^2 + 3/4S^4(^2(^4
E((P)^3 =9/2 S^4 (^2(^4 +15/18 S^6(^3(^6
Первые два момента могут быть взяты для нормального распределения и получим одну аппроксимацию. А если использовать и третий момент, то это распределение Корниш-Фишера которое затабулировано и это будет другое приближение.
Вопрос
24. Обзор простейших моделей и их приложение.
Модель — мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую информацию об этом объекте. Модель является средством познания.
По способу предъявления учащимся такие модели делятся на демонстрационные и раздаточные (индивидуальные). Для усвоения нескольких свойств одного и того же объекта или явления могут существовать несколько моделей, каждая из которых отражает какое-то одно свойство. Например, одну форму, только связи или отношения и т.п. Наиболее широкое распространение в учебном процессе получили идеальные модели (схемы, чертежи, уравнения, выражения, таблицы, плакаты, карточки-задания и др.) К тому же в своей работе учителю приходится строить:
А) модели изучаемого раздела конкретной учебной дисциплины, которые он использует для планирования учебной работы;
Б) модель урока или какого-либо другого занятия, т.е. его план-конспект;
В) модель формирования умственных действий в виде учебной карты, где схематически перечислены все операции, которые надо выполнить для осуществления поставленной цели.
Построение математических моделей – непрерывный процесс, так как любое творчество в математике связано с созданием новых моделей.
Вопрос
Функциональное отношение в теории множеств- это такое отношение между двумя множествами, при котором каждому элементу первого множества может соответствовать не больше одного элемента второго множества.
Определение
Пусть даны два множества Х и У и между ними определено бинарное отношение R. Тогда R назыв. функциональным, если А(перевернутая) принадлежит Х (переверн. А)у1, у2 принадл. У
(хRy) ^ (хRy2) следовательно (у1 = у2)
Замечания
- таким образом если рассматриваемое отношение функционально, то произвольному х принадл. Х может не соответствовать ни один, либо соответствовать в точности один у принадл. Х.
- если функционал. отношение полно слева, то оно назыв. (полной) функцией.
- если функционал. отношение не полно слева, то оно назыв. частичной функцией.
Примеры
- Отношение "явл. полным квадратом" - частичная функция на множестве натур чисел.
- Отношение "явл. квадратным корнем" - полная функция на множестве натур чисел.
ГРАФИКИ ПРОСТЕЙШИХ (элементарных) ФУНКЦИЙ
1. Прямая линия - график линейной функции у=ах+b. Функция монотонно возрастает при а>0 и убывает при а<0.
2. Парабола - график функции квадратного трёхчлена у=ах квадрат + bx+с. Имеет вертик. ось симметрии. Если а>0, имеет мin, а если а<0- мах.
3. Гипербола - график функции у=а деленное на х.
4. Экспонента (показ. функция по основанию е) у=е (вверху х)
5. Логарифмическая функция у=logaX (а>0)
6. у=sinx. Синусоида - периодическая функция с периодом Т=2П.
7. Косинусоида у=cosx.
8. Тангенсоида у=tgx.
Вопрос
Преобразование графиков. Построение графиков сложных функций.
Преобразования графиков функций — это линейные преобразования функции y = f (x) или её аргумента x к виду y = af (kx + b) + m, а также преобразование с использованием модуля.
Зная, как строить графики функции y = f (x), где y = kx + b, y = ax2, y = xn , y = xk, y = sin x, y = cosx, y = tgx, y = ctgx, y = ax  y = logax, можно построить график функции y = af (kx + b) + m.
y = logax, можно построить график функции y = af (kx + b) + m.
| Общий вид функции | Преобразования |
| y = f (x - b) | Параллельный перенос графика вдоль оси абсцисс на | b | единиц
|
| y = f (x + b) |
|
| y = f (x) + m | Параллельный перенос графика вдоль оси ординат на | m | единиц
|
| Отражение графика | |
| y = f (- x) | Симметричное отражение графика относительно оси ординат. |
| y = - f (x) | Симметричное отражение графика относительно оси абсцисс. |
| Сжатие и растяжение графика | |
| y = f (kx) |
|
| y = kf (x) |
|
| Преобразования графика с модулем | |
| y = | f (x) | |
|
| y = f (| x |) |
|
Не нашли, что искали? Воспользуйтесь поиском:
 0 — график остаётся без изменений,
0 — график остаётся без изменений,