Вписанные и описанные многоугольники. Правильные многоугольники

Вписанный в круг многоугольник.

Описанный около кругамногоугольник.

Описанный около многоугольника круг.

Вписанный в многоугольник круг.

Радиус вписанного в треугольник круга.

Радиус описанного около треугольника круга.
Правильный многоугольник.

Центр и апофема правильного многоугольника.
Соотношения сторон и радиусов правильных многоугольников.

Вписанным в круг называется многоугольник, вершины которого расположены на окружности (рис.54). Описанным около круга называется многоугольник, стороны которого являются касательными к окружности

(рис.55).

Соответственно, окружность, проходящая через вершины многоугольника (рис.54), называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными (рис.55), называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него иописать около него окружность. Для треугольника это всегда возможно.

Радиус r вписанного круга выражается через стороны a, b, c треугольника:

Радиус R описанного круга выражается формулой:

В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, если только она равнобочная.

Правильный многоугольник – это многоугольник с равными сторонами и углами.

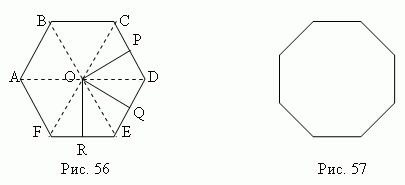
На рис.56 показан правильный шестиугольник, а на рис.57 – правильный восьмиугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º (n – 2) / n, где n – число его углов. Внутри правильного многоугольника существует точка O (рис. 56), равноудалённая от всех его вершин (OA = OB = OC = … = OF), которая называется центром правильного многоугольника. Центр правильного многоугольника также равноудалён от всех его сторон (OP = OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами; отрезки OA, OB, OC, … – радиусы правильного многоугольника. В правильный многоугольник можно вписать окружность и около него можно описать окружность. Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника. Радиус описанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема. Соотношения сторон и радиусов правильных многоугольников:

Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.

П р и м е р. Можно ли вырезать квадрат со стороной 30 см из круга

диаметром 40 см?

Р е ш е н и е. Наибольший квадрат, заключённый в круг, есть вписанный

квадрат. В соответствии с вышеприведенной формулой его

сторона равна:

Следовательно, квадрат со стороной 30 см невозможно вырезать

из круга диаметром 40 см.

Вопрос

--Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям. Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) или B (x0; y0). В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6).

--Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Два отрезка называются равными, если они имеют равные длины.

свойства длины отрезка:

- равные отрезки имеют равные длины;

- меньший отрезок имеет меньшую длину;

- если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.

Длина отрезка определена единственным образом и является неотрицательным числом, равным расстоянию между его концевыми точками.

Сейчас самое время восстановить в памяти четыре определения, которые помогут нам понять способ измерения отрезков.

Если точка A расположена на размеченной прямой, которая называется в этом случае "числовая прямая" (например линейка), то число, соответствующее этой точке, называется ее координатой.

Расстояние между точками А и В на прямой - это модуль разности их координат.

Длина отрезка, определенного A и B, есть модуль разности координат точек A и B.

Два отрезка равны, если они имеют одинаковую длину.

Пусть дан отрезок AB. Если считать линейку частью числовой прямой и расположить AB вдоль линейки так, чтобы точка А совпала с нулем, то точка В будет расположена напротив числа, равного длине AB. Длина AB обозначается АВ.

Вопрос

Не нашли, что искали? Воспользуйтесь поиском: