
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Формула площади равнобедренной трапеции через диагонали и угол между ними
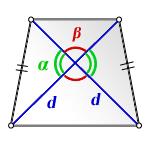
d - диагональ трапеции
α, β - углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
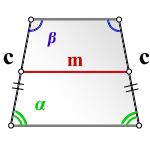
c - боковая сторона
m - средняя линия трапеции
α, β - углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):

5. Формула площади равнобедренной трапеции через основания и высоту
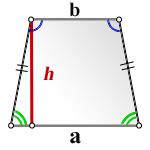
a - нижнее основание
b - верхнее основание
h - высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
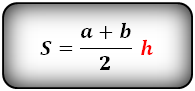
Площадь треугольника по стороне и двум углам, формула.
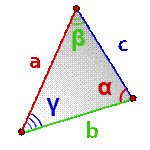
a, b, c - стороны треугольника
α, β, γ - противолежащие углы
Площадь треугольника через сторону и два угла (S):


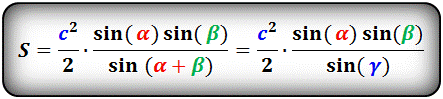
Формула площади правильного многоугольника
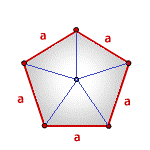
a - сторона многоугольника
n - количество сторон
Площадь правильного многоугольника, (S):
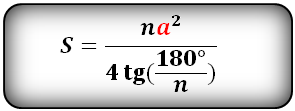
Площадь треугольника, формула Герона

a, b, c, - стороны треугольника
p - полупериметр, p =(a + b + c)/2
Формула (Герона) площади треугольника через полупериметр (S):

Формула расчета площади треугольника
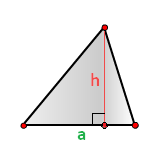
h -высота треугольника
a -основание
Площадь треугольника (S):

Площадь сектора кольца
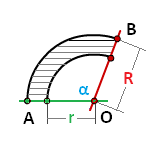
R -радиус внешней окружности
r - радиус внутренней окружности
α - угол сектора AOB, в градусах
π ≈ 3.14
Формула площади сектора кольца (S):

Площадь кольца
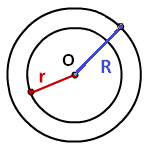
R - радиус внешней окружности
r - радиус внутренней окружности
π ≈ 3.14
Формула площади кольца (S):

Площадь сегмента круга
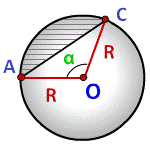
R - радиус круга
α - угол сегмента в градусах
π ≈ 3.14
Формула площади сегмента круга (S), отсекаемая хордой AC:
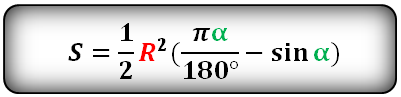
Площадь сектора круга
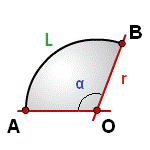
r - радиус круга
L - длина дуги AB
α - угол сектора круга AOB в градусах
π ≈ 3.14
Формула площади сектора круга (S), через длину дуги (L):
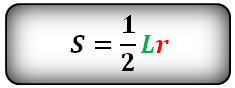
Формула площади сектора круга (S), через угол (α):

Вычислить площадь ромба
 a - сторона ромба
a - сторона ромба
D -большая диагональ
d -меньшая диагональ
α - острый угол
β - тупой угол
Формулы площади ромба (S):
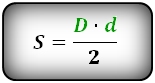


Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
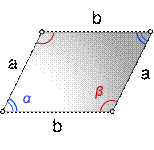
a, b - стороны параллелограмма
α, β - углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
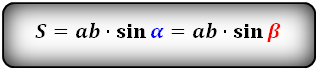
2. Формула площади параллелограмма через сторону и высоту
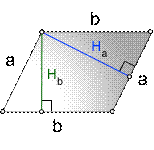
a, b - стороны параллелограмма
H b - высота на сторону b
H a - высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
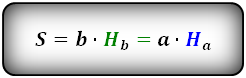
3. Формула площади параллелограмма через диагонали и угол между ними

D -большая диагональ
d -меньшая диагональ
α, β - углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними, (S):

Найти площадь треугольника, угол и две стороны
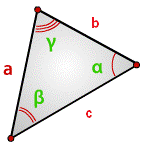
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a, b, c - стороны треугольника
α, β, γ - углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
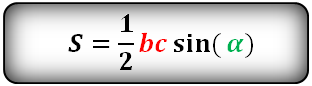

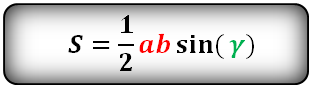
Площадь равностороннего треугольника равна:
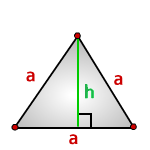
Формулы расчета, площади равностороннего треугольника.
a - сторона треугольника
h - высота
Площадь треугольника через сторону a и высоту h, (S):
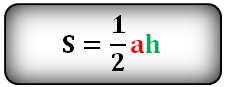
Площадь треугольника только через сторону a, (S):
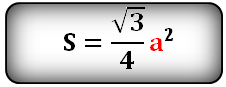
Площадь треугольника только через высоту h, (S):
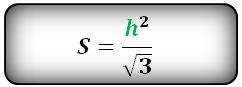
Начало формы
Конец формы
Как вычислить площадь равнобедренного треугольника?
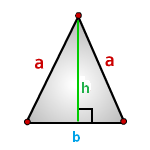
b - основание треугольника
a - равные стороны
h - высота
Формула площади треугольника через высоту h иоснование b, (S):
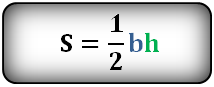
Формула площади треугольника через, стороны a, b, (S):
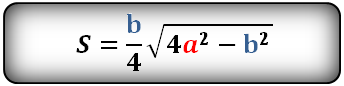
Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a, b - катеты треугольника
Формула площади прямоугольного треугольника, (S):
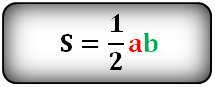
Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
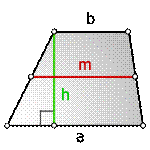
a - нижнее основание
b - верхнее основание
m - средняя линия
h - высота трапеции
Формула площади трапеции, (S):

2. Формула площади трапеции через диагонали и угол между ними
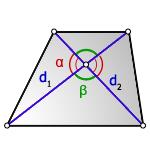
d1, d2 - диагонали трапеции
α, β - углы между диагоналями
Формула площади трапеции, (S):
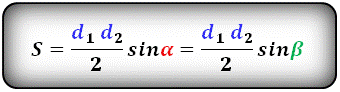
3. Формула площади трапеции через четыре стороны
a - нижнее основание
b - верхнее основание
c, d - боковые стороны
Формула площади трапеции, (S):

Как рассчитать площадь квадрата через диагональ или сторону
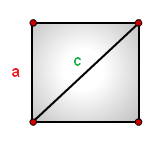
a - сторона квадрата
c - диагональ
Формула площади квадрата через сторону a, (S):

Формула площади квадрата через диагональ c, (S):
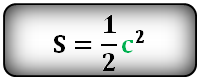
Формула расчета площади прямоугольника

b - длина прямоугольника
a - ширина
Площадь прямоугольника, (S):

Формула площади круга, диаметр
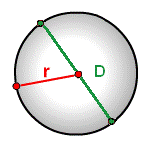
Зная диаметр или радиус круга, можно найти его площадь.
r - радиус круга
D - диаметр
π ≈ 3.14
Формула площади круга, (S):
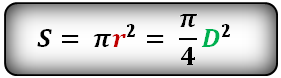
Вопрос
32. уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Вопрос
33. Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат  ,
,  и
и 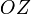 . Оси координат пересекаются в точке
. Оси координат пересекаются в точке 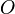 , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей.
, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей.  —ось абсцисс
—ось абсцисс 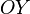 — ось ординат,
— ось ординат, 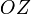 — ось аппликат.
— ось аппликат.


Положение точки  в пространстве определяется тремя координатами
в пространстве определяется тремя координатами  ,
, 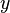 и
и 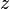 . Координата
. Координата  равна длине отрезка
равна длине отрезка  , координата
, координата 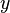 — длине отрезка
— длине отрезка 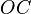 , координата
, координата 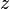 — длине отрезка
— длине отрезка  в выбранных единицах измерения. Отрезки
в выбранных единицах измерения. Отрезки 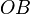 ,
, 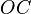 и
и  определяются плоскостями, проведёнными из точки
определяются плоскостями, проведёнными из точки  параллельно плоскостям
параллельно плоскостям 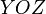 ,
, 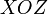 и
и 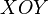 соответственно.
соответственно.
Координата  называется абсциссой точки
называется абсциссой точки  ,
,
координата 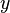 — ординатой точки
— ординатой точки  ,
,
координата 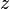 — аппликатой точки
— аппликатой точки  .
.
Символически это записывают так:

или
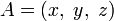
или привязывают запись координат к конкретной точке с помощью индекса:
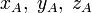
и т. п.
Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка 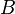 лежала не как на рисунке — на луче
лежала не как на рисунке — на луче  , а на его продолжении в обратную сторону от точки
, а на его продолжении в обратную сторону от точки 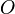 (на отрицательной части оси
(на отрицательной части оси  ), то абсцисса
), то абсцисса  точки
точки  была бы отрицательной (минус расстоянию
была бы отрицательной (минус расстоянию 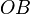 ). Аналогично и для двух других осей.
). Аналогично и для двух других осей.
Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси  против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси
против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси 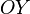 , если этот поворот наблюдать со стороны положительного направления оси OZ)
, если этот поворот наблюдать со стороны положительного направления оси OZ)
Вопрос
34. не уверена в правильности
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях. Как найти длину вектора?
1. Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
2. После этого нужно возвести каждую координату вектора в квадрат.
3. Затем складываем квадраты координат.
4. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 - 1; -1 - 6;7 - 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Вопрос
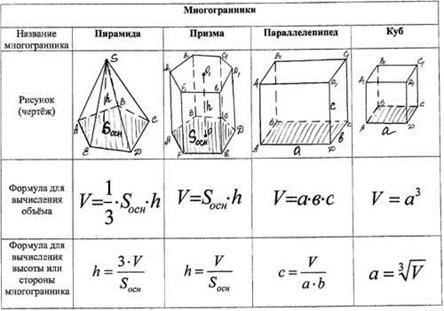
Вычисление площади полной поверхности простейших тел.
Инструкция
1Если нужно вычислить площадь поверхности пола прямоугольной комнаты или прямоугольного же земельного участка, измерьте их длину и ширину. Результаты перемножьте. В этом случае площадь поверхности вычисляется по формуле S=ab, где S - площадь поверхности, а и b — стороны прямоугольника. Формула площади квадрата будет выглядеть как S=a2.
2Если плоская поверхность имеет более сложную форму, ее необходимо разделить на более простые части, формулы вычисления площади которых вам известны. Например, неправильный многоугольник можно разделить на треугольники или несколько треугольников и прямоугольник. При этом учитывайте заданные в условиях задачи параметры многоугольника.
3Если вы имеете дело не с плоскостными фигурами, а с геометрическими телами, действовать необходимо точно так же. В условиях задачи обычно заданы параметры фигуры, которую надо построить или рассчитать. Внимательно прочитайте условия, какую именно площадь вам надо найти. Почти у каждого геометрического тела есть полная площадь поверхности, площадь боковой поверхности и площадь одного или двух оснований.
4Вычислите площадь оснований. У конуса и пирамиды основание одно. Основание пирамиды представляет собой многоугольник и вычисляется по соответствующей формуле. Площадь основания правильной четырехугольной пирамиды вычислите по формуле площади квадрата, то есть возведя в квадрат длину одной из ее сторон. Если в основании пирамиды лежит сложный многоугольник, разделите его на более простые с известными вам параметрами. В основании конуса лежит круг, а соответственно, площадь рассчитывается по формуле S=πR2.
5Найдите площадь боковой поверхности. У прямоугольного параллелепипеда она вычисляется по формуле S=p*h, где p – периметр прямоугольника основания, а h – высота. Площадь поверхности куба вычисляется по формуле S=4a2, поскольку боковая поверхность состоит из 4 квадратов.
6Для вычисления боковой поверхности конуса удобнее всего сделать развертку. Найдите длину окружности по заданному радиусу. Она будет равна длине дуги боковой поверхности конуса. По длине дуги вычислите центральный угол, а затем радиус окружности, сектором которой является боковая поверхность конуса. Зная эти величины, найдите площадь сектора, то есть площадь боковой поверхности конуса.
7Для определения полной поверхности того или иного геометрического тела сложите между собой площади боковой поверхности и оснований.
Вычисление поверхностей и объемов тел
| Призма В — площадь основания; В’ — площадь перпендикулярного сечения; h — высота; l — боковое ребро; Р’ — периметр перпендикулярного сечения | Боковая поверхность призмы, Sб
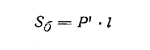
| Объем призмы
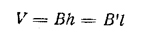
|
| Куб a – ребро; d – диагональ | Полная поверхность куба, Sп

| Объем куба
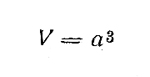
|
| Прямоугольный параллелепипед a, b, c – ребра; d – диагональ | Полная поверхность параллелепипеда, Sб
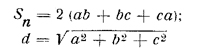
| Объем параллелепипеда

|
| Пирамида В – площадь основания; Р — периметр основания; h — высота; а — апофема (высота боковой грани в правильной пирамиде) | Боковая поверхность пирамиды, Sб

| Объем пирамиды
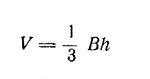
|
| Усеченная пирамида В и b — площади оснований; h — высота; Р и р — периметры оснований; а — апофема | Боковая поверхность усеченной пирамиды, Sб
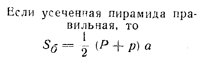
| Объем усеченной пирамиды
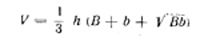
|
| Призма, усеченная плоскостью, не параллельной основанию В’ — площадь перпендикулярного сечения; l — расстояние между центрами тяжести верхнего и нижнего оснований | - | Объем призмы усеченной плоскостью, не параллельной основанию
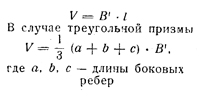
|

Вопрос
Многоугольники относятся к плоским геометрическим фигурам. К объемным (трехмерным) геометрическим фигурам относятся многогранники.
Определение. Многогранник — это геометрическое пространственное тело, ограниченное со всех сторон конечным числом плоских многоугольников (граней).
Прямоугольный параллелепипед является многогранником. Простейший прямоугольный параллелепипед — это куб. У него все грани равны
У прямоугольного параллелепипеда каждая грань — прямоугольник, который имеет с соседней гранью общую сторону и две общие вершины.
У параллелепипеда 8 вершин, 4 боковых прямоугольника и 2 прямоугольника в основаниях. У куба все б граней — равные квадраты. У прямоугольного параллелепипеда боковые фигуры и основания — прямоугольники. Эти прямоугольники попарно равны (равны прямоугольники оснований и две пары противолежащих прямоугольников, составляющих боковые грани). Следовательно, грани прямоугольного параллелепипеда являются прямоугольниками трех типов, различающихся размерами.
Три прямоугольника с разными размерами имеют
одну общую точку — вершину параллелепипеда.
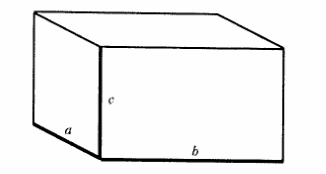
У каждой вершины параллелепипед имеет общую точку для трех отрезков, которые называются измерениями параллелепипеда (длина, ширина и высота). Три измерения на верхнем рисунке параллелепипеда выделены жирной линией.
Объем — это то количество жидкости или сыпучего материала, которое можно поместить внутрь фигуры (между граничными плоскостями).
Объем — это одна из характеристик трехмерных геометрических фигур.
Объем обозначается большой латинской буквой V («вэ»). Величины объема взаимосвязаны (одну кубическую единицу объема можно заменить ругой).
Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
ДЕВОЧКИ,ВОТ ПРИМЕРЫ ЗАДАЧ НА ВСЯКИЙ СЛУЧАЙ!
Примеры
1. Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.
Решение. Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем:
V = 6 * 4 * 8 = 192 (м3)
Ответ: 192 м3.
2. Вычислите объем куба со стороной основания 10 см.
Решение. Подставим численное значение стороны куба в формулу вычисления объема V=а3 и вычислим:
V = 10 * 10 * 10 = 103 = 1 000 (см3) — 1 л.
Ответ: 1 000 см3, или 1 л.
37 вопрос. Вычисление объемов тел вращения.
1. Объем шара равен V=4/3 пиRквадрат.
2. Объем цилиндра равен пиRквадратумноженное на h, гдеh- высота цилиндра
3. Объем усеченного конуса равен 1/3(пиRквадрат+ пиRV+пиrквадрат) где h- высота усеченного конуса, r, R-радиусы оснований
Вопрос





Не нашли, что искали? Воспользуйтесь поиском: