Скалярное произведение векторов. Определение:Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

Определение: Скалярным произведением двух ненулевых векторов и 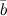называется число, равное произведению длин этих векторов на косинус угла между ними:

Пример: Вычислить скалярное произведение векторов и 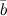, если их длины соответственно равны 2 и 3, а угол между ними 60°.

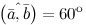Решение. Так как из условия , , а , то

Если хотя бы один из векторов или 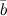равен нулевому вектору, то .

Свойства скалярного произведения:

1° - симметричность.

2° . Обозначается и называется скалярный квадрат.

3° Если , то

4° Если и и , то . Верно и обратное утверждение.

5°

6°

7°

Если векторы и 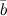заданы своими координатами: , , то их скалярное произведение вычисляется по формуле:

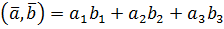
Решение примеров и задач (алгоритм выполнения задания):

Не нашли, что искали? Воспользуйтесь поиском: