Разложение вектора по ортам координатных осей.

Определение: Система ортов (или базисная система векторов) - это система единичных векторов осей координат.

Орт координатной оси обозначается через , оси - через , оси - через (рис. 1).

Для любого вектора 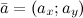, который лежит в плоскости , имеет место следующее разложение: .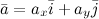

Если вектор расположен в пространстве, то разложение по ортам координатных осей имеет вид: .

Пример: Зная разложение по базисной системе векторов: , записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что

Пример: Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат.

Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе, поэтому искомое разложение:

Не нашли, что искали? Воспользуйтесь поиском: