Теоретический материал. 1. Общие свойства функций.

1. Общие свойства функций.

Определение: Переменная у называется функцией переменной х, если каждому значению х, принадлежащему некоторому множеству Х, поставлено в соответствие единственное значение переменной у.

Определение: Переменная х называется независимой, или аргументом функции, а переменная у – зависимой.

Определение: Множество Х называется областью определения функции Х=(D(y)).

Определение: Графиком функции у=f(x) называется множество точек (х,у) на плоскости, координаты которых удовлетворяют соотношению у=f (x).

Определение: Функция у=f (x) называется чётной, если при любом х Х выполнено равенство f(-x)=f(x).

График чётной функции симметричен относительно оси Оу (оси ординат).

Определение: Функция у=f(x) называется нечётной, если при любом х Х

выполнено равенство f(-x)=-f(x).

График нечётной функции симметричен относительно начала координат.

2. Схема исследования функций:

· Найти область определения функции.

· Установить, не является ли функция четной, нечетной, периодической.

· Найти точки разрыва и исследовать пределы функции в этих точках.

· Найти точки экстремума и значения функции в этих точках.

· Исследовать интервалы возрастания и убывания функции.

Для исследования функции на возрастание и убывание находят производную ƒ΄(х) функции ƒ(х) определяют ее знак. (Если ƒ΄(х) 0, то ƒ(х) возрастает; если ƒ΄(х) 0, то ƒ(х) убывает)

· Найти точки перегиба.

· Исследовать график функции на выпуклость и вогнутость.

· Найти точки пересечения с осями координат.

· Определить промежутки знакопостоянства функции, т.е. промежутки, на которых ƒ(х) 0 и ƒ(х) 0.

· Построить график заданной функции.

Алгоритм решения:

Пример 1. Исследовать функцию у = 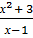и построить ее график. Решение. Область определения функции – вся числовая ось, кроме точки х=1, поэтому, D(у) = (- 1) (1; + ). * Так как у (-х) = = - 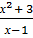, то функция ни четная и ни нечетная. * Так как у(х + Т) = = ни при каком Т 0, то данная функция не периодическая. * Строим прямую х=1. В случае, когда х приближается к 1 слева, значения функции стремятся к – , а в случае, когда х приближается к 1 справа, значения функции стремятся к + . Так как у = 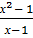+ = х + 1 + , то при |х| 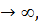график этой функций приближается к графику функции у_{1 =} х +1. * Находим производную у΄ = = и из уравнения - 2х – 3 = 0 определим критические точки: х₁ = - 1 и х₂ = 3. Так как для точек интервала (- ; - 1) производная имеет знак «+», а для точек интервала (- 1; 1) производная имеет знак «-», то точка х₁ = -1 является точкой максимума функции. Аналогично убеждаемся, что точка х₂ = 3 является точкой минимума функции. * Так как уравнение х² + 3 = 0 не имеет действительных корней, то график функции не пересекает ось 0х. * На интервале (- ; - 1) функция возрастает, на интервале (- 1; 1) – убывает, на интервале (1; 3) вновь убывает, на интервале (3; + ) – возрастает.

* Найдем точки графика при х₁ = - 1 и х₂ = 3; А (- 1; - 2); В (3; 6). * Найдем точки пересечения графика функции с осью 0у: у(0) = - 3. * Построим график исходной функции.

у

6 В у = х + 1

-1 3 Х

А -2

-3

х = 1

Пример 2. Исследовать указанную функцию методами дифференциального исчисления и построить её график:

Решение:

1. Функция не определена при х = 5. Область ее определения - (5; ),.

2. Если х=0, то у = 0, график пересекает ось Оу в точке (0; 0). Если у=0, то х₁=0, х₂ = , график пересекает ось Ох в точках (0;0), (; 0).

3. Функция знакоположительна (y> 0) на интервалах и (5; ), знакоотрицательна (y< 0) - (0;5).

4. Функция не является ни четной ни нечетной. .

5. Прямая х = 5 является ее вертикальной асимптотой.

Выясним наличие наклонных асимптот:

горизонтальных асимптот нет.

6. Находим интервалы возрастания и убывания функции:

.

На интервалах (0;0,17) и (7,5;+ ) – функция возрастает, (;0), (0,17;5), (5;7,5) – убывает.

7. (0,17;0,02) – точка максимума;

(0; 0) и (7,5; 652,5) – точки минимума.

8. Исследуем функцию на выпуклость:

;

.

(0,085;0,0009) – точка перегиба.

График выпуклый вверх на интервале (0;085,5), выпуклый вниз – (; 0,085) и (-5; ).

9. Изобразим график функции:

Вопросы для самоконтроля:

1. Что такое функция?

2. Что такое аргумент функции?

3. Что такое график функции?

4. Что такое параллельный перенос графика?

Рекомендуемая литература:

Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.

10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.

11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.

12. Пехлецкий И.Д. Математика: учебник. – М., 2003.

13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. Математика для колледжей» Математический Портал – библиотека math-portal.ru
Тема 8. Многогранники.

Не нашли, что искали? Воспользуйтесь поиском: