Арифметическая прогрессия.

Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность { a_n }, заданная рекуррентно соотношениями

a ₁ = a, a_n = a_{n –1} + d (n = 2, 3, 4, …)(a и d – заданные числа).

Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a ₁ = 1, d = 2.

Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a ₁ = 20, d = –3.

Нетрудно найти явное (формульное) выражение a_n через n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1) d по сравнению с первым членом арифметической прогрессии, т.е.

a_n = a ₁ + d (n – 1).

Это формула n- го члена арифметической прогрессии.

Используя явное выражение a_n через n, можно доказать следующее свойство арифметической прогрессии: если натуральные числа i, j, k, l таковы, что i + j = k + l, то a_i + a_j = a_k + a_l. Чтобы в этом убедиться, достаточно подставить i, j, k и l вместо n в формулу n- го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые n членов арифметической прогрессии, то суммы членов, равно отстоящих от концов, будут одинаковы:

a ₁ + a_n = a ₂ + a_n– 1 = a ₃ + a_n –2 = … = 2 a ₁ + (n – 1) d.

Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии:

S_n = a ₁ + a 2 + … + a_{n –1} + a_n .

С этой целью берется еще одна такая же сумма, но слагаемые записывается в обратном порядке:

S_n = a_n + a_n– 1 + … + a ₂ + a ₁.

Далее она складывается почленно с исходной суммой, причем слагаемые сразу попарно группируются. В результате

2 S_n = (a ₁ + a_n) + (a ₂ + a_{n –1}) + … + (a_n + a ₁) = n (2 a ₁ + (n – 1) d),

откуда . Это формула суммы n членов арифметической прогрессии.

Арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним – предыдущего и последующего. Действительно, так как

a_n = a_{n –1} + d;

a_n = a_{n +1} – d.

двух последних равенств дает .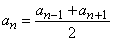

Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.

Пример. При каком значении x числа 3 x + 2, 5 x – 4 и 11 x + 12 образуют конечную арифметическую прогрессию?

Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению

5 x – 4 = ((3 x + 2) + (11 x + 12))/2.

Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3 x + 2, 5 x – 4 и 11 x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.

Не нашли, что искали? Воспользуйтесь поиском: