
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретический материал. Производная функции у = ƒ(х) в точке х0 – это предел отношения приращения функции у в этой точке к соответствующему приращению аргумента х при 0.
Производная функции у = ƒ(х) в точке х0 – это предел отношения приращения функции  у в этой точке к соответствующему приращению аргумента
у в этой точке к соответствующему приращению аргумента  х при
х при  0.
0.
 =
=  =
=  .
.
Производная обозначается у΄ («игрек штрих») или f΄ (х) («эф штрих от икс») или  («де игрек по де икс»).
(«де игрек по де икс»).
dy - «дифференциал функций»  это
это  , т.е. произведение производной функций на дифференциал аргумента.
, т.е. произведение производной функций на дифференциал аргумента.
Правило 1. Производная алгебраической суммы конечного числа  дифференцируемых функций равна алгебраической сумме производных всех этих функций:
дифференцируемых функций равна алгебраической сумме производных всех этих функций:

Правило 2. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй:

Правило 3. Производная произведения постоянного множителя на дифференцируемую функцию равна произведению этого множителя на производную данной функций:
 .
.
Правило 4. Производная частного двух дифференцируемых функций (при условии, что знаменатель не равен 0) равна дроби, числитель которой представляет разность между произведением производной первой функции на вторую и произведением первой функции на производную второй, а знаменатель равен квадрату второй функции:
 .
.
Для нахождения производной функций необходимо сначала применить одно из правил (1, 2,3,4), а потом использовать соответствующую формулу из таблицы производных.
Ниже приведем таблицу производных элементарных функций.
Таблица и правила производных:
| (С)΄ = 0, где С – постоянное число | (Сх)΄ = С х΄ | ||
(υ  ѵ)΄ = υ΄ ѵ)΄ = υ΄  ΄ ΄
| (х)΄ = 1 | ||
| (υѵ)΄= υ΄ѵ + υѵ΄ | ( )΄ = - )΄ = - 
| ||
 ΄ = ΄ = 
| ( )΄ = )΄ = 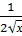
| ||
| (Сυ)΄ = Сυ |  )΄ = )΄ = 
| ||
( )΄ = n )΄ = n 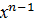
| 15 | (sinх)΄=cоs х | |
( )΄= )΄= 
| (cоs х)΄ = - sin х | ||
 )΄ = )΄ = 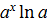
| (tg х)΄ = 
| ||
( )΄= )΄= 
| (ctg х)΄ = - 
|
Решение примеров и задач (алгоритм выполнения задания):
Найдите производные функций:
а)  ; б)
; б)  ; в)
; в) 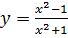 ;
;
г)  ; д)
; д) 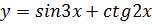 ; е)
; е) 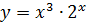 .
.
Решение:
а) 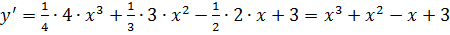 ;
;
б)  ;
;
в)  =
=  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Решите примеры:
1. Найдите производные функций:
а) у =  - 4х + 3; б) у =
- 4х + 3; б) у =  +
+  –
–  +
+  ;
;
в) у =  ; г) у =
; г) у =  .
.
2. Найти производную второго порядка от функции: у = х  sinх.
sinх.
3. В какой момент времени скорость тела, движущегося по закону Ѕ = 3  - 15t + 2, равна 0? Найти ускорение тела.
- 15t + 2, равна 0? Найти ускорение тела.
4.Найти производную первого порядка:
Блок А Блок В
а) у = ех + е-х а) у = 4 е5х - 1
б) у =  + 5
+ 5  + х б) у =
+ х б) у = 
в) у =  в) у =
в) у =  +
+  tgх
tgх
г) у =  sin х +
sin х +  г) у = sin (2х - 1)
г) у = sin (2х - 1)  еах
еах
5. Решить задачи:
а) Тело движется по закону Ѕ =  - 6
- 6  - 4t – 8(м). Определите скорость тела в конце 5 – ой секунды.
- 4t – 8(м). Определите скорость тела в конце 5 – ой секунды.
б) Найти ускорение тела, движущего по закону Ѕ = 0,5  sin 2t (м), при t =
sin 2t (м), при t =  .
.
Вопросы для самоконтроля:
1. Что такое производная функций?
2. Какие способы знаете нахождения производной функций?
3. Что такое «дифференциал функций»?
4. Что такое правило сложение производных?
5. Что такое правило произведение производных?
6. Что такое правило производное частного?
Рекомендуемая литература:
Основные источники:
1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.
2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Дополнительные источники:
1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.
8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
12. Пехлецкий И.Д. Математика: учебник. – М., 2003.
13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.
Интернет ресурсы:
1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307
2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович
e-ypok.ru/content/
3. Математика для колледжей» Математический Портал – библиотека math-portal.ru
Самостоятельная работа №23.
Тема: Решение задач по интегралам (решение примеров и задач).
Время выполнения задания – 6ч.
Цель работы: Закрепление знаний и умений по интегралам с помощью решения примеров и задач.
Не нашли, что искали? Воспользуйтесь поиском: