
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определенный интеграл. Определенный интеграл – это общий предел всех интегральных сумм функции f(х) на отрезке [а, b]
Определенный интеграл – это общий предел всех интегральных сумм функции f (х) на отрезке [ а, b ]. Определенный интеграл обозначается:
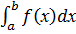 ,
,
где f(х) – подынтегральная функция; х – переменная интегрирования; число а называется нижним пределом интеграла, b – верхним; [ а, b ] – промежуток интегрирования.
Если F(х) – первообразная функция для непрерывной функции у = f(х), т.е. F'(х) = f(х), то имеет место формула:
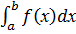 = F(х)|
= F(х)|  = F(b) – F(а).
= F(b) – F(а).
Это формула Ньютона – Лейбница – основная формула интегрального исчисления, устанавливающая связь между определенным и неопределенным интегралом.
Она читается так: Определенный интеграл – это разность значений любой первообразной функции F(b) – F(а), для f(х) при верхнем и нижнем пределах интегрирования.
Разница между определенным и неопределенным интегралами: определенный интеграл – это число, а неопределенный интеграл – это функция.
Основные правила (свойства) определенного интеграла:
При перестановке пределов изменяется знак интеграла:
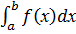 = -
= -  .
.
Интеграл с одинаковыми пределами равен нулю:
 = 0.
= 0.
Отрезок интегрирования можно разбивать на части:
 .
.
Определенный интеграл от алгебраической суммы(разности) функций равен алгебраической сумме(разности) их определенных интегралов:
 =
= 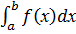

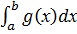 .
.
Постоянный множитель можно выносить за знак определенного интеграла:
 = С
= С 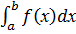 .
.
Если функция f(х)  0 всегда на отрезке [ а; b], то
0 всегда на отрезке [ а; b], то 
Если f (х)  g(х) всюду на отрезке [а; b], то
g(х) всюду на отрезке [а; b], то 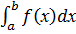

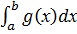 .
.
Геометрический смысл определенного интеграла: он численно равен площади криволинейной трапеции, ограниченной прямыми х = а, х = b и частью графика функции у = f(х), взятой со знаком плюс, если функция положительна, и со знаком минус, если функция отрицательна.
Геометрическая интерпретация определенного интеграла.

Решение примеров и задач (алгоритм выполнения задания):
1.Найти неопределенный интеграл:
Пример 1.
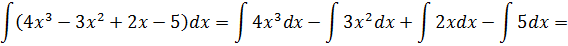
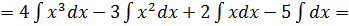 (далее используем таблицу)
(далее используем таблицу)
 .
.
Пример 2.
 , т.к.
, т.к. 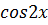 является сложной функций.
является сложной функций.
2.Вычислите определенный интеграл:
Пример 1. Вычислите:  .
.
Решение. Применим формулу Ньютона – Лейбница и свойства определенного интеграла:
 = 3
= 3  =
=  |32 =
|32 =  -
-  = 27 – 8 = 19.
= 27 – 8 = 19.
Пример 2. Вычислите: 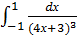 .
.
Решение. Обозначим 4х + 3 = z, откуда 4dх = dz или dх = 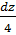 ; при х = – 1, tн = – 4 + 3 = – 1; при х = 1, tв = 4 +3 = 7. Следовательно,
; при х = – 1, tн = – 4 + 3 = – 1; при х = 1, tв = 4 +3 = 7. Следовательно,
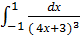 =
=  =
=  =
=  =
=  .
.
Пример 3. Вычислить площадь, ограниченную графиками функций у=  ,у=х.
,у=х.
Решение. Построим графики данных функций, найдя предварительно точки их пересечения путем решения системы: у = х2, у = х. Решив систему, получим точки О (0; 0) и А (1; 1).
у = х2 у=x
А
M
О В
Взяв f(х) = х, вычислим площадь  ОАВ, а взяв f(х) = х2, вычислим площадь криволинейного
ОАВ, а взяв f(х) = х2, вычислим площадь криволинейного  ОMАВ. Затем из первого результата вычтем второй. Итак,
ОMАВ. Затем из первого результата вычтем второй. Итак,
 =
=  |
|  =
=  – 0 =
– 0 =  ;
;  =
=  |
|  =
=  – 0 =
– 0 =  .
.
Следовательно, площадь S фигуры, ограниченная заданными линиями S =  -
-  =
=  (кв.ед.).
(кв.ед.).
Решите примеры:
1.Найти неопределенный интеграл:
а)  ; б)
; б) 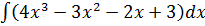 ;
;
в)  ; г)
; г) 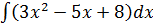 .
.
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ;
;
2.Вычислите определенный интеграл:
1. Вычислите:
а) 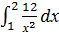 ; б)
; б)  ;в)
;в)  ; г)
; г)  ;д)
;д) 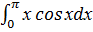 .
.
2. Определить площадь полуволны косинусоиды.
3. Определить площадь, ограниченную графиками функций у=х2 и у=5х.
4. Вычислить площадь фигуры, ограниченной графиком функции у = х3 – 3х2 + 2х – 6, осью 0х и прямыми х = 0 и х = 3.
Вопросы для самоконтроля:
1. Что такое неопределенный интеграл?
2. Какие способы существуют для нахождения неопределенного интеграла?
3. Перечислите основные правила нахождения неопределенного интеграла?
4. Что такое определенный интеграл?
5. Какие способы существуют для вычисления определенного интеграла?
6. Перечислите основные правила вычисления определенного интеграла?
Рекомендуемая литература:
Основные источники:
1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.
2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Дополнительные источники:
1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.
8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
12. Пехлецкий И.Д. Математика: учебник. – М., 2003.
13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.
Интернет ресурсы:
1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307
2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович
e-ypok.ru/content/
3. Математика для колледжей» Математический Портал – библиотека math-portal.ru
Тема 11. Измерения в геометрии.
Не нашли, что искали? Воспользуйтесь поиском: