Математическая статистика.

Пример 1. При измерении веса у 20 случайным образом отобранных студентов были получены следующие результаты (кг): 65, 68, 52, 56, 64, 60, 65, 56, 70, 64, 60, 58, 52, 56, 60, 64, 68, 64, 60, 58. Составить по этим результатам дискретный статистический ряд и построить полигон частот.

Решение: Из полученных результатов измерения можно составить следующую таблицу, таким образом, что первой строке будут все отличающиеся величины начиная с самого меньшего по возрастании, а во второй – частоты их появления соответственно:

	0,10	0,15	0,10	0,20	0,20	0,10	0,10	0,05

Графическим изображением полученного дискретного ряда распределения является полигон частот:

4

3

2

0 52 56 58 60 64 65 68 70

Нетрудно заметить, что статистический дискретный ряд распределения удобно применять при сравнительно небольшом количества отличающихся друг от друга измеряемых величин в выборочной совокупности. Когда это число больше, то результаты представляют в виде статистического интервального ряда распределения.

Для построения такого ряда всю область полученных значений изучаемого параметра необходимо разбить на несколько равных по величине интервалов:

,

где - это величина интервалов, - количество интервалов, а и следовательно минимальное и максимальное значения из выборки.

Пусть - это число значений попадающих в соответствующие интервалы , а - соответствующие относительные частоты. Тогда можно построить следующую таблицу, которую называют статистическим интервальным рядом распределения:

			…
			…
			…
			…

С помощью этой таблицы можно графический изобразить наш ряд распределения, который будем называть гистограммой частот () или относительных частот ().

Определение 4. Гистограммой частот (относительных частот) называется фигура, состоящая из прямоугольников, основаниями которых служат интервалы , а высотами – соответствующие отношения ().

Пример 2. Измеряли величину - рост 50 случайно отобранных студентов. Получили следующие результаты (см): 172, 179, 169, 178, 184, 168, 188, 171, 182, 176, 165, 154, 176, 181, 174, 164, 177, 168, 172, 156, 179, 167, 173, 184, 158, 178, 172, 162, 152, 174, 169, 187, 157, 161, 194, 173, 166, 158, 166, 171, 189, 164, 182, 161, 172, 167, 178, 168, 173, 173.

Построить статистический интервальный ряд распределения, а также гистограмму относительных частот.

Решение: Среди перечисленных значений найдем минимальное и максимальное, т.е. соответственно 152 и 194. Тогда, =194-152=42. Для расчета количества интервалов используем формулу:

.

Ширина каждого интервала равна:

.

Далее составим таблицу:

	152-158	158-164	164-170	170-176	176-182	182-188	188-194
	0,12	0,10	0,20	0,28	0,18	0,08	0,04
	0,02	0,017	0,033	0,047	0,03	0,013	0,007

В выше указанной таблице вычисляем относительные частоты и соответствующие плотности, т. е. полученные значения еще делим на = 6. Далее строим гистограмму относительных частот:

0,047

0,033

0,030

0,020

0,017

0,013

0,007

0 152158164170 176182 188194

Далее на примере рассмотрим полную статистическую обработку.

Пример 3. При измерении веса у 25 случайным образом отобранных студентов были получены следующие результаты (кг): 65, 60, 68, 54, 60, 58, 64, 60, 65, 60, 72, 64, 48, 60, 58, 54, 60, 56, 58, 60, 64, 68, 64, 60, 58.

Проведите полную статистическую обработку.

Решение: Из полученных результатов измерения можно составить следующую таблицу, таким образом, что первой строке будут все отличающиеся величины начиная с самого меньшего по возрастании, а во второй – частоты их появления соответственно:

	0,04	0,08	0,04	0,16	0,32	0,16	0,08	0,08	0,04

Далее определим:

мода – это значение, которое наиболее часто встречается в дискретном вариационном ряде;

медиана - это значение которое находится в середине (в центре) дискретного вариационного рядя и делить ее пополам.

Построить статистический интервальный ряд распределения, а также гистограмму относительных частот.

Среди перечисленных значений найдем минимальное и максимальное, т.е. соответственно 48 и 72. Тогда, =72 - 48=24. Для расчета количества интервалов используем формулу:

.

Ширина каждого интервала равна:

.

Далее составим таблицу:

	48-52	52-56	56-60	60-64	64-68	68-72
	0,04	0,12	0,48	0,16	0,16	0,04
	0,01	0,03	0,12	0,04	0,04	0,01

В выше указанной таблице вычисляем относительные частоты и соответствующие плотности, т. е. полученные значения еще делим на = 4. Далее строим гистограмму относительных частот:

0,047

0,04

0,03

0,01

0 48 525660646872

Вычислим среднее значение:

.

Далее вычислим:

+

+

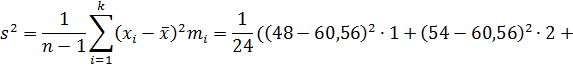
+ 25,9.

Вычислим среднее квадратическое отклонение:

.

Далее вычислим доверительный интервал с доверительной вероятностью :

.

Определим границы доверительного интервала:

нижняя граница - ;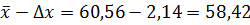

верхняя граница - ;

доверительный интервал – [58,42;62,70].

Окончательно можно записать:

,

Или записать (оценить) с помощью доверительного интервала:

.

Решите примеры:

Задача №1. В коробке лежат пронумерованные шары: 2 шара с цифрой «1»; 4 шара с цифрой «2»; 8 шаров с цифрой «3»; 5 шаров с цифрой «4»; 1 шар с цифрой «5». Составьте таблицу распределения; постройте многоугольник распределения величины – цифра, написанная на шаре. Найдите все параметры дискретной величины (; ; ()).

Задача №2. Изучая случайную величину – успеваемость студентов по математике, анализировали их экзаменационные оценки. Оказалось, что 25% студентов получили оценку «2»; 12,5% – оценку «5». Какая часть студентов получила оценки «3» и «4», если = 3,375?

Задача №3. Случайная величина – число посетителей аптеки за ночь изменяется от 1 до 5. Закон распределения этой величины имеет вид:

	0,06	0,15	0,6	0,15	0,04

Найдите ; ; () и постройте многоугольник распределения.

Задача №4. В коробке лежат пронумерованные шары: 2 шара с цифрой «1»; 4 шара с цифрой «2»; 1 шар с цифрой «3»; 3 шара с цифрой «4». Составьте таблицу распределения; постройте многоугольник распределения величины – цифра, написанная на шаре. Найдите все параметры дискретной величины (; ; ()).

Задача №5. Изучая случайную величину – успеваемость студентов по биологии, анализировали их экзаменационные оценки. Оказалось, что 12% студентов получили оценку – «2»; 15% – оценку «5». Какая часть студентов получила оценки «3» и «4», если = 3,56?

Задача №6. Случайная величина – число посетителей аптеки за ночь изменяется от 0 до 4. Закон распределения этой величины имеет вид:

	0,05	0,11	0,64	0,12	0,08

Найдите ; ; () и постройте многоугольник распределения.

Задача №7. В коробке лежат пронумерованные шары: 3 шара с цифрой «1»; 5 шара с цифрой «2»; 7 шаров с цифрой «3»; 5 шаров с цифрой «4». Составьте таблицу распределения; постройте многоугольник распределения величины – цифра, написанная на шаре. Найдите ее все параметры.

Задача №8. Изучая случайную величину – успеваемость студентов по физике, анализировали их экзаменационные оценки. Оказалось, что 35% студентов получили оценку «3»; 15% - оценку «4». Какая часть студентов получила оценки «2» и «5», если = 2,95?

Задача №9. Случайная величина – число посетителей аптеки за ночь. Закон распределения этой величины имеет следующий вид:

	0,07	0,15	0,55	0,15	0,08

Найдите числовые характеристики дискретной случайной величины и постройте многоугольник.

Задача №10. В коробке лежат пронумерованные шары: 2 шара с цифрой «1»; 5 шаров с цифрой «2»; 8 шаров с цифрой «3»; 5 шара с цифрой «4». Составьте таблицу распределения; постройте многоугольник распределения величины – цифра, написанная на шаре. Найдите ее все параметры.

Задача №11. Изучая случайную величину – успеваемость студентов по математике, анализировали их экзаменационные оценки. Оказалось, что 30% студентов получили оценку – «2»; 10% – оценку «5». Какая часть студентов получила оценки «3» и «4», если = 3,15?

Задача №12. Случайная величина – число посетителей аптеки за ночь. Закон распределения имеет следующий вид:

	0,03	0,18	0,62	0,12	0,05

Найдите числовые характеристики дискретной случайной величины и постройте многоугольник.

Задача №13. В коробке лежат шары с номерами: 1 шар с цифрой «2»; 3 – с цифрой «4»; 4 – с цифрой «6»; 2 – с цифрой «8». Составьте таблицу и постройте многоугольник распределения величины. Найдите ее все параметры.

Задача №14. Изучая случайную величину – успеваемость студентов по физике, анализировали их экзаменационные оценки. Оказалось, что 25% студентов получили оценку «2»; 20% – оценку «4». Какая часть студентов получила оценки «3» и «5», если = 3,25?

Задача №15. Случайная величина – число посетителей аптеки за день. Закон распределения этой величины представлен в таблице:

	0,05	0,15	0,60	0,09	0,11

Найдите числовые характеристики дискретной случайной величины и постройте многоугольник.

Не нашли, что искали? Воспользуйтесь поиском: