ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратные уравнения и неравенства.
Квадратное уравнение.
Дискриминант: 
Если D > 0, то кв. ур-е имеет два различных корня: 
которые могут быть вычислены по формулам:
или
Если D = 0, то кв. ур-е имеет единственный корень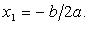 
. Если D < 0, то действительных корней нет.
Частные случаи
1. 
(приведенное квадратное уравнение), 
при D > 0
при D = 0
2. 
при D > 0
при D = 0
3. 
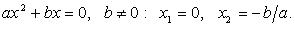
4. 
5. 
Если 
- корни квадратного уравнения 
то
Для уравнения 
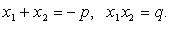
Разложение квадратного трехчлена на множители
Если D > 0, то 
Если D = 0, то 
Квадратичные неравенства
D - дискриминант, 
- корни квадратного уравнения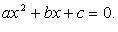 
.
1. 
.
2. 
.
Неравенства 
и 
сводятся к рассмотренным умножением на -1.
Частные случаи
Биквадратное уравнение
Сводится к квадратному уравнению заменой 
Не нашли, что искали? Воспользуйтесь поиском: